题目内容
13．在同一坐标系中，函数y=-$\frac{k}{x}$和y=kx+1的图象大致是（ ）| A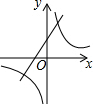． |  | B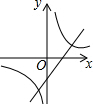． |  | C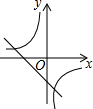． |  | D． |  |
分析 据一次函数和反比例函数的特点，k≠0，所以分k＞0和k＜0两种情况讨论即可．
解答 解：分两种情况讨论：
①当k＞0时，y=kx+1与y轴的交点在正半轴，过一、二、三象限，y=-$\frac{k}{x}$的图象在第二、四象限；
②当k＜0时，y=kx+1与y轴的交点在正半轴，过一、二、四象限，y=-$\frac{k}{x}$的图象在第一、三象限．
故选：D．
点评 本题主要考查了反比例函数的图象性质和一次函数的图象性质，关键是由k的取值确定函数所在的象限．
练习册系列答案
相关题目
3．下列各式的计算中，结果为2$\sqrt{5}$的是（ ）
| A． | $\sqrt{2}×\sqrt{10}$ | B． | $\sqrt{8}×\sqrt{5}$ | C． | $\sqrt{10}÷\sqrt{2}$ | D． | $\sqrt{\frac{1}{2}}÷\sqrt{\frac{1}{80}}$ |
如图，直径为10的⊙A经过点C（0，6）和点O（0，0），B是y轴右侧圆弧上一点，则cos∠OBC=$\frac{4}{5}$．
如图，点D是三角形ABC外一点，过点D分别作DE∥BC，DF∥AC，分别交AC、BC于点E，F，求证：∠D=∠C．
18．
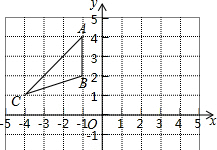已知△ABC在直角坐标系中的位置如图所示，如果△A′B′C′与△ABC关于y轴对称，那么点C的对应点C′的坐标为（ ）
已知△ABC在直角坐标系中的位置如图所示，如果△A′B′C′与△ABC关于y轴对称，那么点C的对应点C′的坐标为（ ）| A． | （-4，1） | B． | （-4，-1） | C． | （4，-1） | D． | （4，1） |
5．下列命题中是真命题的是（ ）
| A． | 对角线互相垂直且相等的四边形是正方形 | |
| B． | 平分弦的直径垂直于弦 | |
| C． | 两条对角线相等的平行四边形是矩形 | |
| D． | 两边相等的平行四边形是菱形 |
3．计算$\sqrt{2\frac{1}{4}}$的结果是（ ）
| A． | $\frac{3}{2}$ | B． | $±2\frac{1}{2}$ | C． | $±\frac{3}{2}$ | D． | 2$\frac{1}{2}$ |