题目内容
2.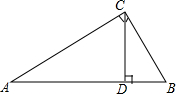 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.
分析 根据在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,可得AB的长,然后根据∠ACB=90°,CD⊥AB,可以得到∠ACD、∠BCD与∠A、∠B的关系,从而可以解答本题.
解答 解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{(\sqrt{5})^{2}+{2}^{2}}$=$\sqrt{9}=3$,∠CDA=CDB∠=90°.
∴∠ACD+∠A=∠A+∠B=90°,∠BCD+∠B=∠B+∠A=90°.
∴∠ACD=∠B,∠BCD=∠A.
∵sinA=$\frac{BC}{AB}=\frac{2}{3}$,sinB=$\frac{AC}{AB}=\frac{\sqrt{5}}{3}$,
∴sin∠ACD=$\frac{\sqrt{5}}{3}$,sin∠BCD=$\frac{2}{3}$.
点评 本题考查解直角三角形,解题的关键是建立各个角之间的关系,根据相等角的正弦值相等,利用转化的数学思想解答本题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
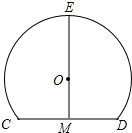 如图,是一个灯罩的横截面,它的形状是以点O为圆心的圆的一部分,点M是⊙O中弦CD的中点,EM经过圆心交⊙O于点E,EM=CD=8cm,则⊙O的半径为5cm.
如图,是一个灯罩的横截面,它的形状是以点O为圆心的圆的一部分,点M是⊙O中弦CD的中点,EM经过圆心交⊙O于点E,EM=CD=8cm,则⊙O的半径为5cm.