题目内容
7.若一直角三角形的一直角边与斜边的比为4:5,且斜边长是20,则此三角形的另一直角边长是12.分析 利用一直角三角形的一直角边与斜边的比为4:5,且斜边长是20,得出直角边的长,再利用勾股定理得出答案.
解答 解:∵一直角三角形的一直角边与斜边的比为4:5,且斜边长是20,
∴设这条直角边长为4x,斜边长为:5x,
则5x=20,
解得:x=4,
故4x=16,即这条直角边长为16,
则此三角形的另一直角边长是:$\sqrt{2{0}^{2}-1{6}^{2}}$=12.
故答案为:12.
点评 此题主要考查了勾股定理,根据题意正确应用勾股定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 将一副三角板按如图所示摆放,则∠ABC的度数为( )
将一副三角板按如图所示摆放,则∠ABC的度数为( )
 将一副三角板按如图所示摆放,则∠ABC的度数为( )
将一副三角板按如图所示摆放,则∠ABC的度数为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
15.计算$\frac{b}{a}$•$\frac{{a}^{2}-a}{b}$的结果是( )
| A. | a+1 | B. | a-1 | C. | ab-1 | D. | ab-b |
17.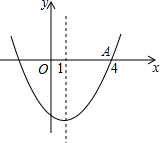 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )| A. | (-4,0) | B. | (-3,0) | C. | (-2,0) | D. | (-1,0) |
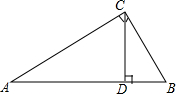 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.