题目内容
13．已知多边形的每个内角与其外角的差均为90°，求每个内角的度数与多边形的边数．分析 一个多边形的每个内角都相等，每个内角与每个外角的差是90°，则每个外角是45°．正多边形的外角和是360°，这个正多边形的每个外角相等，因而用360°除以外角的个数，就得到外角和中外角的个数，外角的个数就是多边形的边数．再根据多边形的内角和定理就可以求出这个多边形的内角和．
解答 解：设每一个外角为x°，则每一个内角为（x+90）°，
根据题意，得x+x+90=180，
解得x=45，
x+90=135，
360÷45=8．
答：每个内角的度数为135°，它的边数为8．
点评 本题考查了多边形的内角与外角．根据正多边形的外角和求多边形的边数是常用的一种方法，需要熟记．
练习册系列答案
小学期末标准试卷系列答案
相关题目
3．若两个有理数的和为负数，那么这两个有理数（ ）
| A． | 一定是负数 | B． | 一正一负，且负数的绝对值大 | ||
| C． | 一个为零，另一个为负数 | D． | 至少有一个是负数 |
如图，在直角梯形ABCD中，DC∥AB，∠DAB=90°，AC⊥BC，AC=BC，∠ABC的平分线分别交AD、AC于点E，F，则（1）$\frac{AB}{AC}$的值是$\sqrt{2}$；（2）$\frac{BF}{EF}$的值是$\sqrt{2}+1$．
18．
将一副三角板按如图所示摆放，则∠ABC的度数为（ ）
将一副三角板按如图所示摆放，则∠ABC的度数为（ ）| A． | 70° | B． | 75° | C． | 80° | D． | 85° |
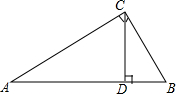如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AC=$\sqrt{5}$，BC=2，求sin∠ACD和sin∠BCD．
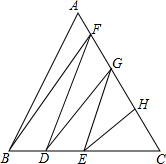如图所示，等边三角形ABC的边长是100cm，用折线把这个等边三角形分割成面积相等的六个三角形，那么图中CD+CG的长是多少？