题目内容
12.已知二次函数y=ax2+bx+3(a≠0)图象的对称轴是直线x=2,且经过点B(3,0).(1)求这个二次函数的解析式;
(2)若y>0,请直接写出x的取值范围;
(3)若抛物线y=ax2+bx+3-t(a≠0,t为实数)在$0<x<3\frac{1}{2}$的范围内与x轴有公共点,求出t的取值范围.
分析 (1)由抛物线的对称性可求得点B对称点的坐标,从而然后依据待定系数法可求得二次函数的解析式;
(2)y>0,即抛物线位于x轴上方,从而可求得x的取值范围;
(3)由(1)可知y=ax2+bx+3-t的解析式为y=x2-4x+3-t,当△=0时,可求得t=-1,将x=0,y=0代入可求得t=3,从而可得到-1≤t<3.
解答 解:(1)∵对称轴为x=2,点B(3,0),
∴抛物线经过点(1,0).
将(1,0)、(3,0)代入得:9a+3b+3=0且a+b+3=0
解得a=1,b=-2
∴y=x2-4x+3.
(2)∵y>0,
∴抛物线位于x轴的上方.
∴x的取值范围是x<1或x>3.
(3)由(1)ax2+bx+c=x2-4x+3
∴y=x2-4x+3-t
①当△=0时,该函数图象与x轴只有一个交点
此时,△=(-4)2-4(3-t)=0
即4+4t=0
∴t=-1
②当该函数图象过(0,0)时,
将(0,0)代入y=x2-4x+3-t
0=3-t
∴t=3
∴t的取值范围是:-1≤t<3.
点评 本题主要考查的是抛物线与x轴的交点,利用数形结合思想求得x和t的取值范围是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
20.某农场经过两年的时间将产量从200万斤提高到260万斤,其中第二年增产的百分率是第一年的2倍.设第一年增产的百分率为x,则可列方程为( )
| A. | 200(1+x)(1+2x)=260 | B. | 200(1+2x)2=260 | ||
| C. | 200(1+x)+200(1+2x)2=260 | D. | 200(1+x)2=260 |
17.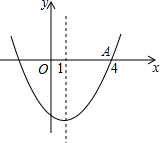 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )| A. | (-4,0) | B. | (-3,0) | C. | (-2,0) | D. | (-1,0) |
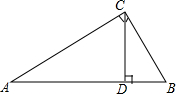 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.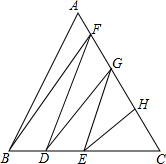 如图所示,等边三角形ABC的边长是100cm,用折线把这个等边三角形分割成面积相等的六个三角形,那么图中CD+CG的长是多少?
如图所示,等边三角形ABC的边长是100cm,用折线把这个等边三角形分割成面积相等的六个三角形,那么图中CD+CG的长是多少?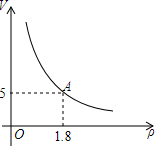 如图,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,求:
如图,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,求: