题目内容
12.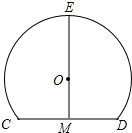 如图,是一个灯罩的横截面,它的形状是以点O为圆心的圆的一部分,点M是⊙O中弦CD的中点,EM经过圆心交⊙O于点E,EM=CD=8cm,则⊙O的半径为5cm.
如图,是一个灯罩的横截面,它的形状是以点O为圆心的圆的一部分,点M是⊙O中弦CD的中点,EM经过圆心交⊙O于点E,EM=CD=8cm,则⊙O的半径为5cm.
分析 连接OC,由垂径定理可知OM⊥CD,在Rt△COM中,由OC2=CM2+OM2,进而可求得半径OC.
解答 解:如图所示,连接OC.
∵M是⊙O弦CD的中点,
∴EM⊥CD,
∵CD=8,
∴CM=$\frac{1}{2}$CD=4.
设圆的半径是xcm,
在Rt△COM中,由勾股定理得:OC2=CM2+OM2,即:x2=42+(8-x)2,
解得:x=5,
所以圆的半径长是5cm.
故答案为:5cm.
点评 本题主要考查的是垂径定理、勾股定理的应用,利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
2.重庆悬挑玻璃景观廊桥,修建在重庆云阳龙缸景区,比世界闻名的美国科罗拉多大峡谷玻璃廊桥悬挑还长5米多,被誉为世界第一悬挑玻璃景观廊桥.“十•一”黄金周期间,龙缸廊桥景区在7天假期中每天接待游客的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数为m万人,则10月2日的游客人数为(m+2.4)万人;
(2)七天内游客人数最大的是10月3日;
(3)若9月30日游客人数为2万人,门票每人180元.请求出黄金周期间龙缸廊桥景区票总收入是多少万元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化(万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.4 |
(2)七天内游客人数最大的是10月3日;
(3)若9月30日游客人数为2万人,门票每人180元.请求出黄金周期间龙缸廊桥景区票总收入是多少万元?
3.若两个有理数的和为负数,那么这两个有理数( )
| A. | 一定是负数 | B. | 一正一负,且负数的绝对值大 | ||
| C. | 一个为零,另一个为负数 | D. | 至少有一个是负数 |
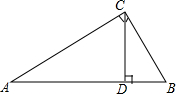 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.