题目内容
10.(1)已知x-3y=0,求$\frac{2x+y}{{x}^{2}-2xy+{y}^{2}}$•(x-y)的值;(2)已知a=3b,b=2c(c≠0),求$\frac{2a-b+3c}{a+4b-5c}$的值.
分析 (1)先对所求的式子化简,然后根据x-3y=0得到x与y的关系,从而可以解答本题;
(2)根据a=3b,b=2c(c≠0),可以建立a、b与c的关系,然后代入所求的式子即可解答本题.
解答 解:(1)$\frac{2x+y}{{x}^{2}-2xy+{y}^{2}}$•(x-y)
=$\frac{2x+y}{(x-y)^{2}}•(x-y)$
=$\frac{2x+y}{x-y}$,
∵x-3y=0,
∴x=3y,
∴原式=$\frac{2×3y+y}{3y-y}=\frac{7y}{2y}=\frac{7}{2}$,
即$\frac{2x+y}{{x}^{2}-2xy+{y}^{2}}$•(x-y)的值是$\frac{7}{2}$;
(2)∵a=3b,b=2c(c≠0),
∴a=6c,b=2c,
∴$\frac{2a-b+3c}{a+4b-5c}$=$\frac{2×6c-2c+3c}{6c+4×2c-5c}=\frac{13c}{9c}=\frac{13}{9}$,
即$\frac{2a-b+3c}{a+4b-5c}$的值是$\frac{13}{9}$.
点评 本题考查分式的化简求值,解题的关键是对所求式子能化简的先化简,然后根据题目中的信息,灵活变化,得到所求问题需要的条件.

练习册系列答案
相关题目
18. 将一副三角板按如图所示摆放,则∠ABC的度数为( )
将一副三角板按如图所示摆放,则∠ABC的度数为( )
 将一副三角板按如图所示摆放,则∠ABC的度数为( )
将一副三角板按如图所示摆放,则∠ABC的度数为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
15.计算$\frac{b}{a}$•$\frac{{a}^{2}-a}{b}$的结果是( )
| A. | a+1 | B. | a-1 | C. | ab-1 | D. | ab-b |
20.某农场经过两年的时间将产量从200万斤提高到260万斤,其中第二年增产的百分率是第一年的2倍.设第一年增产的百分率为x,则可列方程为( )
| A. | 200(1+x)(1+2x)=260 | B. | 200(1+2x)2=260 | ||
| C. | 200(1+x)+200(1+2x)2=260 | D. | 200(1+x)2=260 |
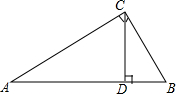 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=$\sqrt{5}$,BC=2,求sin∠ACD和sin∠BCD.