题目内容
20.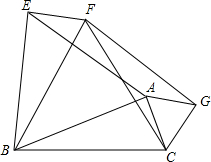 如图,以△ABC的三边为一边的BC的同侧作等边三角形△ABE,△BCF,△ACG.求证:四边形AEFG是平行四边形.
如图,以△ABC的三边为一边的BC的同侧作等边三角形△ABE,△BCF,△ACG.求证:四边形AEFG是平行四边形.
分析 根据等边三角形的性质得出边角之间的关系,再利用全等三角形的判定得出△FBE≌△CBA,进而得出EF=AG,同理可得AE=GF,即可得出四边形ADFE为平行四边形.
解答 证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BF=BC,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
$\left\{\begin{array}{l}{BF=BC}\\{∠FBE=∠CBA}\\{EB=AB}\end{array}\right.$
∴△FBE≌△CBA(SAS).
∴EF=AC,
又∵△AGC为等边三角形,
∴CG=AG=AC.
∴EF=AG.
同理可得AE=GF.
∴四边形AEFG是平行四边形.
点评 此题主要考查了全等三角形的判定与性质以及平行四边形的判定,得出EF=AG是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若a≠b,下列各式中不能成立的是( )
| A. | (a+b)2=(-a-b)2 | B. | (-a-b)(a-b)=(b+a)(b-a) | C. | (a-b)2n=(b-a)2n | D. | (a-b)3=(b-a)3 |
 如图,在a上找到M、N两点,且MN=10mm,M在N的左边,使四边形ABMN的周长最短.
如图,在a上找到M、N两点,且MN=10mm,M在N的左边,使四边形ABMN的周长最短. 如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长.
如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长. 如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形.
如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形. 如图,弦AB的长为6,线段OF分别平分弦AC、弦AB和$\widehat{AC}$,D、F为交点,BD与OC相交于点E.求OE的长.
如图,弦AB的长为6,线段OF分别平分弦AC、弦AB和$\widehat{AC}$,D、F为交点,BD与OC相交于点E.求OE的长.