题目内容
9. 如图,弦AB的长为6,线段OF分别平分弦AC、弦AB和$\widehat{AC}$,D、F为交点,BD与OC相交于点E.求OE的长.
如图,弦AB的长为6,线段OF分别平分弦AC、弦AB和$\widehat{AC}$,D、F为交点,BD与OC相交于点E.求OE的长.
分析 连接BC,根据垂径定理得到OF⊥AC,根据三角形的中位线的性质得到OD∥BC,OD=$\frac{1}{2}$BC,由圆周角定理得到AB是⊙O的直径,通过△ODE∽△BCE,得到$\frac{OE}{CE}=\frac{OD}{BC}$=$\frac{1}{2}$,即可得到结论.
解答  解:连接BC,
解:连接BC,
∵线段OF分别平分弦AC、和$\widehat{AC}$,
∴OF⊥AC,
∵OF分别平分弦AC、弦AB,
∴OD∥BC,OD=$\frac{1}{2}$BC,
∴∠ACB=90°,
∴AB是⊙O的直径,
∴OC=OB=3,
∵OD∥BC,
∴△ODE∽△BCE,
∴$\frac{OE}{CE}=\frac{OD}{BC}$=$\frac{1}{2}$,
∴OE=$\frac{1}{3}$OC=1.
点评 本题考查了圆周角定理,三角形的中位线的性质,垂径定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,在3×3的正方形ABCD中,由A向各交叉点引连线,构成∠1,2,…∠9,则这9个角的和为405度.
如图,在3×3的正方形ABCD中,由A向各交叉点引连线,构成∠1,2,…∠9,则这9个角的和为405度.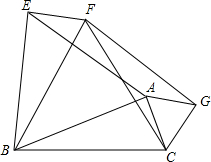 如图,以△ABC的三边为一边的BC的同侧作等边三角形△ABE,△BCF,△ACG.求证:四边形AEFG是平行四边形.
如图,以△ABC的三边为一边的BC的同侧作等边三角形△ABE,△BCF,△ACG.求证:四边形AEFG是平行四边形. (1)请在如图中的坐标系中画出函数y=x2-x和y=x+1的图象;
(1)请在如图中的坐标系中画出函数y=x2-x和y=x+1的图象; 如图,直线AB,CD被直线EF所截,且∠1=60°,∠2=120°,那么AB与CD平行吗?为什么?
如图,直线AB,CD被直线EF所截,且∠1=60°,∠2=120°,那么AB与CD平行吗?为什么? 知图,有一块长80cm,宽60cm的长方形硬纸片,在四角各剪去一个同样的小正方形,用剩余部分做成一个底面积为1500cm2的无盖的长方体盒子,求剪去的小正方形的边长.
知图,有一块长80cm,宽60cm的长方形硬纸片,在四角各剪去一个同样的小正方形,用剩余部分做成一个底面积为1500cm2的无盖的长方体盒子,求剪去的小正方形的边长.