题目内容
16.化简:$\sqrt{8{x}^{3}{y}^{2}}$=2xy$\sqrt{2x}$.分析 先根据性质展开,再根据二次根式的性质把根式化成最简根式即可.
解答 解:原式=$\sqrt{{2}^{2}•2•{x}^{2}•x•{y}^{2}}$
=$\sqrt{{2}^{2}}$•$\sqrt{{x}^{2}}$•$\sqrt{{y}^{2}}$•$\sqrt{2x}$
=2xy$\sqrt{2x}$.
故答案为:2xy$\sqrt{2x}$.
点评 本题考查了二次根式的性质的应用,主要考查学生运用性质进行化简的能力,注意:当x≥0时,$\sqrt{{x}^{2}}$=x,

练习册系列答案
相关题目
4.若分式$\frac{x-2y}{x+y}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 是原来的3倍 | B. | 不变 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |
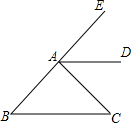 如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.
如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.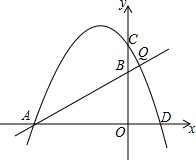 设直线y=$\frac{1}{2}$x+2与抛物线y=-$\frac{1}{2}$x2-x+4交于点A,点Q,若在x轴上方的抛物线上只存在相异的两点M、N,S△MAQ=S△NAQ=S,则S的取值范围$\frac{15}{2}$<S<$\frac{125}{16}$.
设直线y=$\frac{1}{2}$x+2与抛物线y=-$\frac{1}{2}$x2-x+4交于点A,点Q,若在x轴上方的抛物线上只存在相异的两点M、N,S△MAQ=S△NAQ=S,则S的取值范围$\frac{15}{2}$<S<$\frac{125}{16}$.