题目内容
7.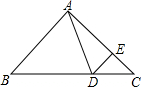 如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
分析 (1)先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+60°=105°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论;
(2)利用(1)的思路与方法解答即可.
解答 解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=105°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC.
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=105°-∠EDC=45°+∠EDC,
解得:∠CDE=30°;
(2)∠CDE=$\frac{1}{2}$∠BAD,
理由:设∠BAD=x,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=45°+x,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠CDE,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠CDE=45°+x-∠CDE=45°+∠CDE,
得:∠CDE=$\frac{1}{2}$∠BAD.
点评 本题考查的是三角形外角的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
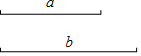 已知:线段a,b.
已知:线段a,b. 如图,DE,BC被那条直线所截,得到哪些同位角,内错角或同旁内角?请一一指出.
如图,DE,BC被那条直线所截,得到哪些同位角,内错角或同旁内角?请一一指出.