题目内容
18.化简:(1)$\sqrt{\frac{121}{36}}$;(2)$\sqrt{1\frac{1}{9}}$
(3)$\sqrt{\frac{81{x}^{2}}{25{y}^{2}}}$(x≥0,y>0).
分析 (1)直接利用二次根式的性质化简求出答案;
(2)直接利用二次根式的性质化简求出答案;
(3)直接利用二次根式的性质化简求出答案.
解答 解::(1)$\sqrt{\frac{121}{36}}$=$\frac{11}{6}$;
(2)$\sqrt{1\frac{1}{9}}$=$\sqrt{\frac{10}{9}}$=$\frac{\sqrt{10}}{3}$;
(3)$\sqrt{\frac{81{x}^{2}}{25{y}^{2}}}$(x≥0,y>0)
=$\frac{9x}{5y}$.
点评 此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
3.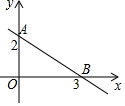 如图,直线AB对应的函数表达式是( )
如图,直线AB对应的函数表达式是( )
 如图,直线AB对应的函数表达式是( )
如图,直线AB对应的函数表达式是( )| A. | y=-$\frac{3}{2}$x+2 | B. | y=$\frac{3}{2}$x+3 | C. | y=-$\frac{2}{3}$x+2 | D. | y=$\frac{2}{3}$x+2 |
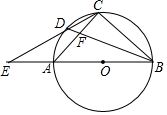 如图,AB是⊙O的直径,点D是$\widehat{AC}$的中点,CD与BA的延长线交于E,BD与AC交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AC}$的中点,CD与BA的延长线交于E,BD与AC交于点F.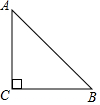 如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.
如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.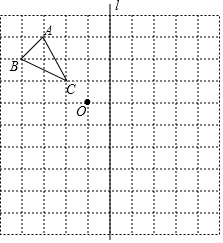 如图,在边长为1个单位长度的正方形网格中,有一个格点△ABC(各个顶点都是正方形网格的格点).
如图,在边长为1个单位长度的正方形网格中,有一个格点△ABC(各个顶点都是正方形网格的格点).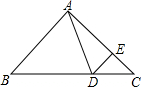 如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.