题目内容
10.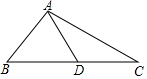 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 根据相似三角形的判定定理得到△ACD∽△BCA,根据相似三角形的性质列出比例式,计算即可.
解答 解:∵AD是中线,BC=8,
∴CD=$\frac{1}{2}$BC=4,
∵∠B=∠DAC,∠C=∠C,
∴△ACD∽△BCA,
∴$\frac{CD}{CA}$=$\frac{CA}{CB}$,即$\frac{4}{CA}$=$\frac{CA}{8}$,
解得,AC=4$\sqrt{2}$,
故选:B.
点评 本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
 如图所示,平面直角坐标系中,△ABC的边AB在x轴上,∠C=60°,AC交y轴于点E,AC,BC的长是方程x2-16x+64=0的两个根且OA:OB=1:3,请解答下列问题:
如图所示,平面直角坐标系中,△ABC的边AB在x轴上,∠C=60°,AC交y轴于点E,AC,BC的长是方程x2-16x+64=0的两个根且OA:OB=1:3,请解答下列问题: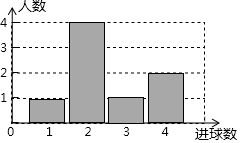 体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.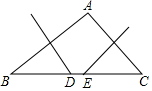 如图,△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是10cm.
如图,△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是10cm.
 如图,直线l同侧有A、B两点,请利用直尺和圆规在直线l上求作一点P,使AP+BP值最小.(不写作法,保留作图痕迹)
如图,直线l同侧有A、B两点,请利用直尺和圆规在直线l上求作一点P,使AP+BP值最小.(不写作法,保留作图痕迹)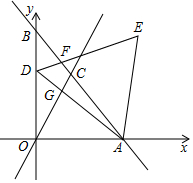 如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.
如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.