题目内容
2.已知|a|=5,b2=4,(1)若a>0,b<0,求a+b的值;
(2)若ab<0,求2a-3b的值.
分析 根据绝对值的性质和有理数的乘方的计算法则得到a,b的值;
(1)由于a>0,b<0,可求a=5,b=-2,再代入计算即可求解;
(2)根据有理数的乘法可得a=5,b=-2或a=-5,b=2,再代入计算即可求解.
解答 解:∵|a|=5,b2=4,
∴a=±5,b=±2,
(1)∵a>0,b<0,
∴a=5,b=-2,
∴a+b=5+(-2)=3;
(2)∵ab<0,
∴a=5,b=-2或a=-5,b=2,
所以2a-3b=16或-16.
点评 此题考查了绝对值的性质和有理数的乘方,有理数的加法和乘法,关键是得到a,b的值.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12.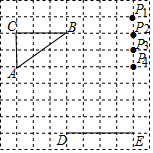 如图,在方格纸中,△ABC和△DPE的顶点均在格点上,要使△ABC∽△DPE,则点P所在的格点为( )
如图,在方格纸中,△ABC和△DPE的顶点均在格点上,要使△ABC∽△DPE,则点P所在的格点为( )
 如图,在方格纸中,△ABC和△DPE的顶点均在格点上,要使△ABC∽△DPE,则点P所在的格点为( )
如图,在方格纸中,△ABC和△DPE的顶点均在格点上,要使△ABC∽△DPE,则点P所在的格点为( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
10.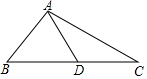 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
14.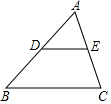 如图,DE∥BC,在下列比例式中,不能成立的是( )
如图,DE∥BC,在下列比例式中,不能成立的是( )
 如图,DE∥BC,在下列比例式中,不能成立的是( )
如图,DE∥BC,在下列比例式中,不能成立的是( )| A. | $\frac{AB}{AD}$=$\frac{AC}{AE}$ | B. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | C. | $\frac{AD}{DB}$=$\frac{DE}{BC}$ | D. | $\frac{AD}{DE}$=$\frac{AB}{BC}$ |
 如图,已知一次函数y=-$\frac{3}{4}$x+3的图象与x轴和y轴分别相交于A,B两点,点C在AB上,以1个单位/s的速度从点B向A运动,同时点D在线段AO上以同样的速度从点A向O运动,运动时间用t(s)表示.
如图,已知一次函数y=-$\frac{3}{4}$x+3的图象与x轴和y轴分别相交于A,B两点,点C在AB上,以1个单位/s的速度从点B向A运动,同时点D在线段AO上以同样的速度从点A向O运动,运动时间用t(s)表示.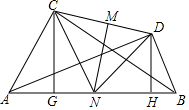 已知:如图,∠ACB=∠ADB=90°,M、N分别是CD、AB的中点,连结CN、DN,过点C作CG⊥AB,过点D作DH⊥AB,恰好有CG=NH.
已知:如图,∠ACB=∠ADB=90°,M、N分别是CD、AB的中点,连结CN、DN,过点C作CG⊥AB,过点D作DH⊥AB,恰好有CG=NH.