题目内容
13.已知x2-4x+y2-$\frac{1}{2}$y+$\frac{65}{16}$=0,求x2-4$\sqrt{y}$的值.分析 根据题目中的式子可以求得x、y的值,从而可以解答本题.
解答 解:∵x2-4x+y2-$\frac{1}{2}$y+$\frac{65}{16}$=0,
∴$(x-2)^{2}+(y-\frac{1}{4})^{2}=0$,
∴x-2=0,y-$\frac{1}{4}$=0,
解得,x=2,y=$\frac{1}{4}$,
∴x2-4$\sqrt{y}$
=${2}^{2}-4\sqrt{\frac{1}{4}}$
=4-2
=2.
点评 本题考查配方法的应用、非负数的性质,解题的关键是明确它们各自的含义.

练习册系列答案
相关题目
15.已知一个圆锥的侧面积是底面积的2倍,圆锥的母线长为2,则圆锥的底面半径是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
18.已知方程x2+kx+6=0的两个根比方程x2-kx+6=0的两个根都大5,那么k的值是( )
| A. | -5 | B. | 5 | C. | 0 | D. | 1 |
3.下列等式成立的是( )
| A. | (-a)2=a2 | B. | a+a=a2 | C. | -2+3=-1 | D. | 3a+5b=8ab |
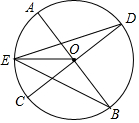 如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB.
如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB. 把如图所示的图形分成4个全等的图形.
把如图所示的图形分成4个全等的图形.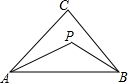 如图,P是△ABC内一点,求证:∠APB>∠ACB.
如图,P是△ABC内一点,求证:∠APB>∠ACB.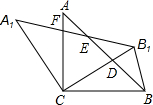 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F