��Ŀ����
5��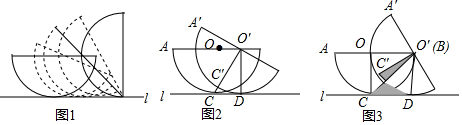 ��ͼ1��һ���뾶Ϊ2�İ�Բ��ƽ��������˳ʱ�����������ƽ�濴��ֱ��l����ʼλ�õİ�ԲO��ֱ��l�����ڵ�C��AB��l�����������У���ԲO����ֱ��l�����ڵ�D����A��B��C�ڰ�ԲO���ϵĶ�Ӧ��ֱ�ΪA�䡢B�䡢C�䣮
��ͼ1��һ���뾶Ϊ2�İ�Բ��ƽ��������˳ʱ�����������ƽ�濴��ֱ��l����ʼλ�õİ�ԲO��ֱ��l�����ڵ�C��AB��l�����������У���ԲO����ֱ��l�����ڵ�D����A��B��C�ڰ�ԲO���ϵĶ�Ӧ��ֱ�ΪA�䡢B�䡢C�䣮��1����ͼ2����˳ʱ�����30��ʱ������C��O��D=30�㣬��CD��
��2����ͼ3�����������У���O��ǡ�þ�����B��
����ֱ��д��CD=2��
�����������C��O��D��
��ͼ3�У�������Ӱ����ֱ�ΪS1��S2��
��ֱ��д��S1��S2�Ĵ�С��ϵΪ��S1��S2�����������=��������
��ֱ��д��S1+S2=$\frac{��}{3}$+2-$\sqrt{2}$���������������У�
���� ��1���ú�30���ֱ��������ֱ�Ӽ��㼴�ɣ�
��2����ͬ��1���ķ������㼴�ɣ�����������˳ʱ������ĽǶ�֮�ͼ��ɵó����ۣ��۷ֱ�������κ������ε����ֱ�ӱȽϴ�С����ͼ��ɣ�
��� �⣺��1����Rt��CO'D�У���C��O��D=30�㣬O'D=r=2��
��O'D=$\sqrt{3}$CD��
��CD=$\frac{2\sqrt{3}}{3}$��
��2���١ߵ�O��ǡ�þ�����B��
��OO'=O'D=OC=CD=2��
�ʴ�Ϊ2��
�ڡ�OO'=O'D=OC=CD=2��
���ı���OCDO'�����Σ�
�ߡ�OCD=90�㣬
���ı���OCDO'�������Σ�
��O'C�ǶԽ��ߣ�
���CO'D=45�㣬
�ߡ�C'O'D'=30�㣬
���DOC'=��CO'D+��C'O'D'=75�㣬
����ͼ3��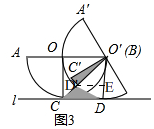 �ߡ�C'O'D'=30�㣬
�ߡ�C'O'D'=30�㣬
��S1=$\frac{30��•{2}^{2}}{360}$=$\frac{��}{3}$��1
����D'��D'E��OD��
��Rt��O'D'E�У�O'D'=2����EO'D'=45�㣬
��O'E=$\frac{\sqrt{2}}{2}$O'D'=$\sqrt{2}$��
��DE=O'D-O'E=2-$\sqrt{2}$��
��S2=$\frac{1}{2}$CD•DE=$\frac{1}{2}$��2����2-$\sqrt{2}$��=2-$\sqrt{2}$��1��
��S1��S2��S1+S2=$\frac{��}{3}$+2-$\sqrt{2}$
�ʴ�Ϊ������$\frac{��}{3}$+2-$\sqrt{2}$
���� ������Բ���ۺ��⣬��Ҫ���������ε�����������������ʽ�������ε��ж����Ȿ��Ĺؼ����ҳ�˳ʱ������ĽǶȣ����������ȱ������ι�����������ת������Բ�ϣ���һ���ѶȲ���ĺ��⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| ��ˮ��/�� | ���ۣ�Ԫ/m3�� |
| ������20m3 | 3 |
| ����20m3�IJ��� | 4 |
| ����ÿ��������ˮ����0.2Ԫ�ij�����ˮ������ | |
��2�����ij�û�2�·ݹ�����ˮ��80Ԫ����ô���û�2�·���ˮ���������ף�
��3�������û�ˮ��3�·ݳ��˹��ϣ�ֻ��70%����ˮ������ˮ���У��������û���3�·�ֻ������58.8Ԫˮ�ѣ���ô���û�3�·�ʵ��Ӧ�ý���ˮ�Ѷ���Ԫ��
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\sqrt{2}$ | D�� | $\frac{3}{2}$ |
 ��1���߹���ͼ������ABC�����Բ��O����������ͼ�ۼ�����д������
��1���߹���ͼ������ABC�����Բ��O����������ͼ�ۼ�����д������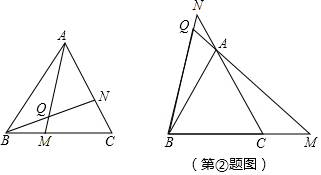
 ��ͼ����A��������y=x2-4x�Գ����ϵ�һ�㣬����OA����AΪ��ת���Ľ�AO��ʱ����ת90��õ�AO�䣬��O��ǡ��������������ʱ����A������Ϊ��2��-1����2��2����
��ͼ����A��������y=x2-4x�Գ����ϵ�һ�㣬����OA����AΪ��ת���Ľ�AO��ʱ����ת90��õ�AO�䣬��O��ǡ��������������ʱ����A������Ϊ��2��-1����2��2����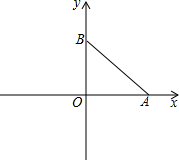 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B���������ֱ�Ϊ
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B���������ֱ�Ϊ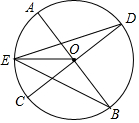 ��ͼ����֪��AB��CD�ǡ�O������ֱ����EΪ$\widehat{AC}$���е㣬��֤��EOƽ�֡�DEB��
��ͼ����֪��AB��CD�ǡ�O������ֱ����EΪ$\widehat{AC}$���е㣬��֤��EOƽ�֡�DEB��