题目内容
6. 如图.已知二次函数y=ax2+bx(α≠0)经过点A(-2,0),B(-3,3).
如图.已知二次函数y=ax2+bx(α≠0)经过点A(-2,0),B(-3,3).(1)求二次函数的解析式;
(2)一次函数y=kx+6的图象经过点B交二次函数的图象于点D,写出使一次函数值小于二次函数值的x的取值范围.
分析 (1)利用待定系数法求二次函数的解析式;
(2)先列方程组可求出点D的坐标,利用图象可得结论.
解答  解:(1)把A(-2,0),B(-3,3)代入y=ax2+bx得:
解:(1)把A(-2,0),B(-3,3)代入y=ax2+bx得:
$\left\{\begin{array}{l}{4a-2b=0}\\{9a-3b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
∴二次函数的解析式为:y=x2+2x;
(2)把B(-3,3)代入y=kx+6中得:3=-3k+6,
k=1,
∴一次函数的解析式为:y=x+6,
则$\left\{\begin{array}{l}{y=x+6}\\{y={x}^{2}+2x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=3}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=8}\end{array}\right.$,
∴D(2,8),
由图象得:当x>2或x<-3时,一次函数值小于二次函数值.
点评 本题考查了利用待定系数法求二次函数和一次函数的解析式,属于常考题型,要熟练掌握;本题还利用了数形结合的思想,求函数值大小关系时所对应的x的取值范围.

练习册系列答案
相关题目
17.“水是生命之源”,某城市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
(1)如果某用户1月份用水量为19m3,那么该用户1月份应该缴纳水费多少元.
(2)如果某用户2月份共缴纳水费80元,那么该用户2月份用水多少立方米?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,那么该用户3月份实际应该缴纳水费多少元?
| 用水量/月 | 单价(元/m3) |
| 不超过20m3 | 3 |
| 超过20m3的部分 | 4 |
| 另:每立方米用水加收0.2元的城市污水处理费 | |
(2)如果某用户2月份共缴纳水费80元,那么该用户2月份用水多少立方米?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,那么该用户3月份实际应该缴纳水费多少元?
11.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+2y=3}\\{3x+5y=m+2}\end{array}\right.$的解满足x+y=0,求有理数m的值.
15.已知一个圆锥的侧面积是底面积的2倍,圆锥的母线长为2,则圆锥的底面半径是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
 (1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)
(1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)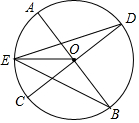 如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB.
如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB. 如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点.将△ACD绕点C逆时针旋转90°到△BCE.
如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点.将△ACD绕点C逆时针旋转90°到△BCE.