题目内容
3.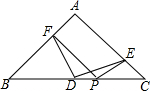 如图,Rt△ABC中,∠BAC=90°,AB=AC,D为BC的中点,P为BC上一点,PF⊥AB于F,PE⊥AC于E,则DF与DE的关系为DF=DE且DF⊥ED.
如图,Rt△ABC中,∠BAC=90°,AB=AC,D为BC的中点,P为BC上一点,PF⊥AB于F,PE⊥AC于E,则DF与DE的关系为DF=DE且DF⊥ED.
分析 如图,连接AD.欲证明DF=DE,只要证明△ADF≌△CDE即可.
解答 解:如图,连接AD.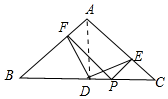
∵AB=AC,∠BAC=90°,BD=DC,
∴AD=BD=DC,∠C=∠BAD=45°,
∵PE⊥AB,PF⊥AC,
∴∠AFP=∠AEP=∠EAF=90°,
∴四边形AFPE是矩形,∠C=∠EPC=45°,
∴PE=AF,PE=EC,
∴AF=EC,
在△ADF和△CDE中,
$\left\{\begin{array}{l}{AD=DC}\\{∠FAD=∠C}\\{AF=EC}\end{array}\right.$,
∴△ADF≌△CDE,
∴DF=DE,∠FDA=∠EDP,
∴∠FDE=∠ADC=90°
故答案为DF=DE且DF⊥DE.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、矩形的判定和性质等知识,解题的关键是灵活运用所学知识,正确寻找全等三角形,属于中考常考题型.

练习册系列答案
相关题目
11.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+2y=3}\\{3x+5y=m+2}\end{array}\right.$的解满足x+y=0,求有理数m的值.
15.已知一个圆锥的侧面积是底面积的2倍,圆锥的母线长为2,则圆锥的底面半径是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
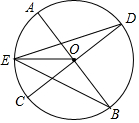 如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB.
如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB.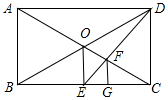 如图,在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则线段BG与GC的数量关系是BG=2CG.
如图,在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则线段BG与GC的数量关系是BG=2CG. 把如图所示的图形分成4个全等的图形.
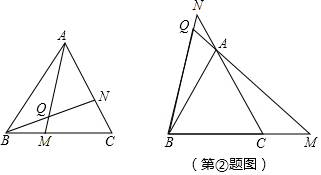
把如图所示的图形分成4个全等的图形.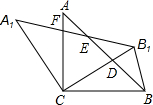 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F