题目内容
 如图,在△ABC中,AC=BC,以腰AC、BC为边向外作等边△ACD和△BCE,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:
如图,在△ABC中,AC=BC,以腰AC、BC为边向外作等边△ACD和△BCE,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:(1)△ABD≌△BAE;
(2)CG是线段AB的垂直平分线.
考点:全等三角形的判定与性质,线段垂直平分线的性质,等边三角形的性质
专题:证明题
分析:(1)根据等腰三角形和等边三角形的性质,证明AD=BE,∠DAB=∠CBA,由AB=AB,证明△ABD≌△BAE;
(2)先证明点F在AB的垂直平分线上,再证明点C在AB的垂直平分线上,从而证明CG是线段AB的垂直平分线.
(2)先证明点F在AB的垂直平分线上,再证明点C在AB的垂直平分线上,从而证明CG是线段AB的垂直平分线.
解答:证明:(1)∵AC=BC,
∴∠CAB=∠CBA,
∵△ACD和△BCE是等边三角形,
∴∠DAC=∠CBE=60°,AD=AC,BE=AC,
∴AD=BE,
∴∠CAB+∠DAC=∠CBA+∠CBE,
即:∠DAB=∠CBA,
在△ABD和△BAE中,
,
∴△ABD≌△BAE(SAS);
(2)∵△ABD≌△BAE,
∴∠EAB=∠DBA,
∴点F在AB的垂直平分线上,
又∵CA=CB,
∴点C在AB的垂直平分线上,
∴CF是线段AB的垂直平分线,
即CG是线段AB的垂直平分线.
∴∠CAB=∠CBA,
∵△ACD和△BCE是等边三角形,
∴∠DAC=∠CBE=60°,AD=AC,BE=AC,
∴AD=BE,
∴∠CAB+∠DAC=∠CBA+∠CBE,
即:∠DAB=∠CBA,
在△ABD和△BAE中,
|
∴△ABD≌△BAE(SAS);
(2)∵△ABD≌△BAE,
∴∠EAB=∠DBA,
∴点F在AB的垂直平分线上,
又∵CA=CB,
∴点C在AB的垂直平分线上,
∴CF是线段AB的垂直平分线,
即CG是线段AB的垂直平分线.
点评:本题考查了全等三角形的性质和判定、等腰或等边三角形的性质以及线段垂直平分线的性质和判定,解题的关键是结合图形寻找证明三角形全等的条件,另外证明直线是线段的垂直平分线,必须证明直线上的两个点都在线段的垂直平分线上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等腰△ABC内接于半径为5的⊙O,如果底边BC的长为6,则底角的正切值为( )
| A、3 | ||||
B、
| ||||
C、3或
| ||||
D、3或
|
抛物线y=2+6x-x2的顶点坐标为( )
| A、(3,11) | ||||
| B、(-3,-25) | ||||
C、(
| ||||
| D、(6,2) |
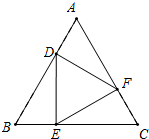 如图,点D、E、F分别在等边△ABC的三边AB、BC、CA上,且△DEF也是等边三角形,求证:AD=BE=CF.
如图,点D、E、F分别在等边△ABC的三边AB、BC、CA上,且△DEF也是等边三角形,求证:AD=BE=CF. 如图,已知线段AB=12cm,线段BC=4cm,D是线段AB的中点,E是线段BC的中点,则线段DE长为
如图,已知线段AB=12cm,线段BC=4cm,D是线段AB的中点,E是线段BC的中点,则线段DE长为 如图,图①所示的正方体木块,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,分别画出②从正面看、从左面看和从上面看到的平面图形.
如图,图①所示的正方体木块,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,分别画出②从正面看、从左面看和从上面看到的平面图形.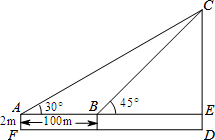 如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)
如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)