题目内容
1.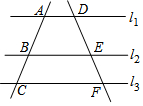 如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.
如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.
分析 利用平行线分线段成比例定理得到$\frac{AB}{AC}$=$\frac{DE}{DF}$,然后把有关数据代入计算即可.
解答 解:∵l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,
∴$\frac{AB}{AC}$=$\frac{DE}{DF}$,
∵$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,
∴$\frac{4}{7}$=$\frac{2}{DF}$,
解得:DF=3.5,
∴EF=DF-DE=3.5-2=1.5.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
相关题目
12.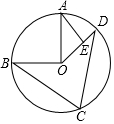 如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
 如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
6.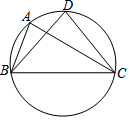 如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
 如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )| A. | 70° | B. | 50° | C. | 45° | D. | 30° |
13.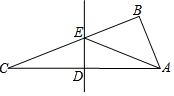 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
10.下列计算正确的是( )
| A. | (-x2)3=-x6 | B. | x4•x2=x8 | C. | (x3)2=-x5 | D. | x3•x2=2x6 |
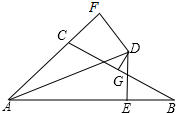 如图∠BAC的平分线AD与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=22,AC=10,则BE=6.
如图∠BAC的平分线AD与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=22,AC=10,则BE=6.