题目内容
12．
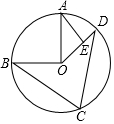如图，点A，B，C，D是⊙O上顺次4点，OA⊥OB，AE⊥OD于E，当∠C=70°时，∠A的度数是（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |
分析 由圆周角定理得出∠BOD=2∠C=140°，由题意得出∠AOB=∠AEO=90°，求出∠AOE=50°，由直角三角形的性质得出∠A=40°即可．
解答 解：∵∠C=70°，
∴∠BOD=2∠C=140°，
∵OA⊥OB，AE⊥OD，
∴∠AOB=∠AEO=90°，
∴∠AOE=140°-90°=50°，
∴∠A=90°-50°=40°；
故选：C．
点评 此题考查了圆周角定理、直角三角形的性质；熟练掌握圆周角定理是解决问题的关键．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
2．下列各数比-2015小的是（ ）
| A． | 2015 | B． | 0 | C． | -2014 | D． | -2016 |
3．
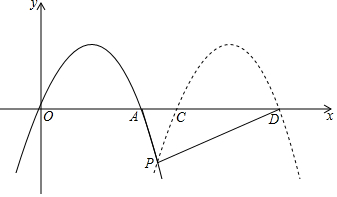如图，抛物线y=-2x2+4x与x轴的另一个交点为A，现将抛物线向右平移m（m＞2）个单位长度，所得抛物线与x轴交于C，D，与原抛物线交于点P，设△PCD的面积为S，则用m表示S正确的是（ ）
如图，抛物线y=-2x2+4x与x轴的另一个交点为A，现将抛物线向右平移m（m＞2）个单位长度，所得抛物线与x轴交于C，D，与原抛物线交于点P，设△PCD的面积为S，则用m表示S正确的是（ ）| A． | $\frac{m}{2}$（m2-4） | B． | $\frac{1}{2}$m2-2 | C． | $\frac{m}{2}$（4-m2） | D． | 2-$\frac{1}{2}$m2 |
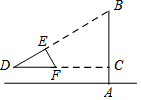如图，小南用自制的直角三角形纸板DEF测量树的高度AB，他使斜边DF保持水平，并且边DE与点B在同一直线上．己知三角形的两条直角边DE=0.6m，EF=0.3m，测得边DF离地面的高度AC=1.5m，CD=8m，求树高AB．
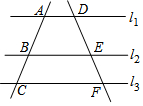如图，直线l1∥l2∥l3，直线AC依次交l1、l2、l3于A、B、C三点，直线DF依次交l1、l2、l3于D、E、F三点，若$\frac{AB}{AC}$=$\frac{4}{7}$，DE=2，求EF的长．
如图，已知等边△ABC．