题目内容
6.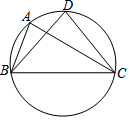 如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )| A. | 70° | B. | 50° | C. | 45° | D. | 30° |
分析 根据三角形内角和定理求出∠A,根据圆周角定理求出∠D,求出∠DBC=∠DCB,根据三角形内角和定理求出即可.
解答 解:∵在△ABC中,∠ABC=70°,∠ACB=30°,
∴∠A=180°-∠ABC-∠ACB=80°,
∴∠D=∠A=80°,
∵D是弧BAC的中点,
∴$\widehat{BD}$=$\widehat{CD}$,
∴∠DBC=∠DCB,
∴∠DBC=$\frac{1}{2}$(180°-∠D)=50°,
故选B.
点评 本题考查了三角形内角和定理,圆周角定理,圆心角、弧、弦之间的关系等知识点,能根据定理求出∠D=∠A和∠DCB=∠DBC是解此题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
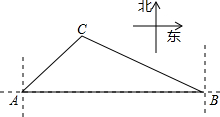 如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.
如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.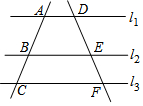 如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.
如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.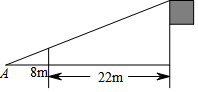 如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
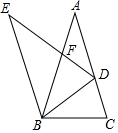 如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.
如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.