题目内容
20.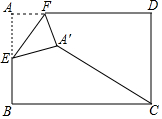 如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.
如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.
分析 连接CE,根据折叠的性质可知A′E=1,在Rt△BCE中利用勾股定理可求出CE的长度,再利用三角形的三边关系可得出点A′在CE上时,A′C取最小值,最小值为CE-A′E=$\sqrt{10}$-1,此题得解.
解答 解:连接CE,如图所示.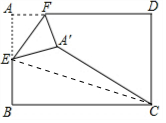
根据折叠可知:A′E=AE=$\frac{1}{2}$AB=1.
在Rt△BCE中,BE=$\frac{1}{2}$AB=1,BC=3,∠B=90°,
∴CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\sqrt{10}$.
∵CE=$\sqrt{10}$,A′E=1,
∴点A′在CE上时,A′C取最小值,最小值为CE-A′E=$\sqrt{10}$-1.
故答案为:$\sqrt{10}$-1.
点评 本题考查了翻折变换、矩形的性质、勾股定理以及三角形的三边关系,利用三角形的三边关系可得出点A′在CE上时,A′C取最小值是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
11.三角形的两边长分别为4和9,则它的第三边长可以为( )
| A. | 4 | B. | 5 | C. | 9 | D. | 13 |
15. 某中学九年级学生进行了五次体育模拟测试,甲同学的测试
某中学九年级学生进行了五次体育模拟测试,甲同学的测试
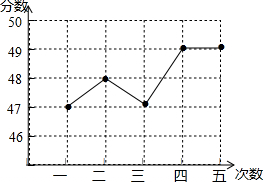
成绩如表,乙同学的测试成绩折线统计图如图所示:
(1)请根据甲、乙两同学五次体育模拟测试的成绩填写下表:
(2)在图中用虚线画出甲测试成绩的折线统计图;
(3)甲、乙两位同学在这五次体育模拟测试中,谁的成绩较为稳定?谁的成绩一直呈上升趋势.
 某中学九年级学生进行了五次体育模拟测试,甲同学的测试
某中学九年级学生进行了五次体育模拟测试,甲同学的测试成绩如表,乙同学的测试成绩折线统计图如图所示:
| 次 数 | 一 | 二 | 三 | 四 | 五 |
| 分 数 | 46 | 47 | 48 | 49 | 50 |
| 中位数 | 平均数 | 方差 | |
| 甲 | 48 | 48 | 2 |
| 乙 | 48 | 48 | 0.8 |
(3)甲、乙两位同学在这五次体育模拟测试中,谁的成绩较为稳定?谁的成绩一直呈上升趋势.
5.平面上有A、B、C三点,其中AB=3,BC=4,AC=5,若分别以A、B、C为圆心,半径长为2画圆,画出圆A,圆B,圆C,则下列叙述何者正确( )
| A. | 圆A与圆C外切,圆B与圆C外切 | B. | 圆A与圆C外切,圆B与圆C外离 | ||
| C. | 圆A与圆C外离,圆B与圆C外切 | D. | 圆A与圆C外离,圆B与圆C外离 |
12.下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(分) | 92 | 95 | 95 | 92 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |



 如图,DE垂直平分△ABC的边BC,CE平分∠ACB,∠BAC=75°,则∠B的度数为35°.
如图,DE垂直平分△ABC的边BC,CE平分∠ACB,∠BAC=75°,则∠B的度数为35°.