题目内容
5.平面上有A、B、C三点,其中AB=3,BC=4,AC=5,若分别以A、B、C为圆心,半径长为2画圆,画出圆A,圆B,圆C,则下列叙述何者正确( )| A. | 圆A与圆C外切,圆B与圆C外切 | B. | 圆A与圆C外切,圆B与圆C外离 | ||
| C. | 圆A与圆C外离,圆B与圆C外切 | D. | 圆A与圆C外离,圆B与圆C外离 |
分析 根据圆和圆的位置与两圆的圆心距、半径的数量之间的关系,即可判定.
解答 解:∵AC=5>2+2,即AC>RA+RB,
∴⊙A与⊙C外离,
∵BC=4=2+2,即BC=RB+RC,
∴⊙B与⊙C相切.
故选C.
点评 本题考查圆与圆的位置关系,记住:①两圆外离?d>R+r;②两圆外切?d=R+r;③两圆相交?R-r<d<R+r(R≥r);④两圆内切?d=R-r(R>r);⑤两圆内含?d<R-r(R>r)是解题的关键.

练习册系列答案
相关题目
15.$\sqrt{(-1)^{2}}$=( )
| A. | -1 | B. | ±1 | C. | 1 | D. | 以上都不对 |
16. 如图,AB∥CD,若∠1=40°,则∠2的度数为( )
如图,AB∥CD,若∠1=40°,则∠2的度数为( )
 如图,AB∥CD,若∠1=40°,则∠2的度数为( )
如图,AB∥CD,若∠1=40°,则∠2的度数为( )| A. | 40° | B. | 150° | C. | 140° | D. | 130° |
13.∠A的补角为125°18′,则它的余角为( )
| A. | 25.7° | B. | 35.3° | C. | 35.7° | D. | 54.7° |
10.如图的数轴上有O、A、B三点,其中O为原点,A点所表示的数为106,根据图中数轴上这三点之间的实际距离进行估计,下列何者最接近B点所表示的数( )


| A. | 2×106 | B. | 4×106 | C. | 2×107 | D. | 4×108 |
17.(-1)+2=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
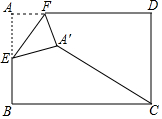 如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.
如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.


