题目内容
8. 如图,DE垂直平分△ABC的边BC,CE平分∠ACB,∠BAC=75°,则∠B的度数为35°.
如图,DE垂直平分△ABC的边BC,CE平分∠ACB,∠BAC=75°,则∠B的度数为35°.
分析 根据线段垂直平分线的性质得到EB=EC,得到∠B=∠ECB,根据三角形内角和定理、角平分线的定义计算即可.
解答 解:∵DE垂直平分△ABC的边BC,
∴EB=EC,
∴∠B=∠ECB,
∵CE平分∠ACB,
∴∠ECB=∠ACE,
∵∠BAC=75°,
∴∠B+∠ACB=105°,
∴∠B=$\frac{1}{3}×$105°=35°,
故答案为:35°.
点评 本题考查的是线段的垂直平分线的性质、角平分线的定义,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
18.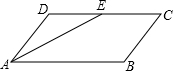 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=10,BC=5,则DE:EC的值( )
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=10,BC=5,则DE:EC的值( )
 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=10,BC=5,则DE:EC的值( )
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=10,BC=5,则DE:EC的值( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | 3:4 |
19. 如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )
如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )
 如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )
如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )| A. | x>3 | B. | x<3 | C. | x≥3 | D. | x≤3 |
16. 如图,AB∥CD,若∠1=40°,则∠2的度数为( )
如图,AB∥CD,若∠1=40°,则∠2的度数为( )
 如图,AB∥CD,若∠1=40°,则∠2的度数为( )
如图,AB∥CD,若∠1=40°,则∠2的度数为( )| A. | 40° | B. | 150° | C. | 140° | D. | 130° |
3.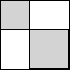 如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )
如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )
 如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )
如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{24}{49}$ | D. | $\frac{25}{49}$ |
13.∠A的补角为125°18′,则它的余角为( )
| A. | 25.7° | B. | 35.3° | C. | 35.7° | D. | 54.7° |
17.(-1)+2=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
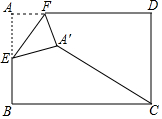 如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.
如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.