题目内容
4.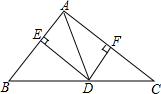 如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.
如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.
分析 根据AD是BC的中线得出S△ABD=S△ACD,根据三角形的面积公式得出$\frac{1}{2}$AB•DE=$\frac{1}{2}$AC•DF,从而求得DE:DF的值.
解答 解:∵AD是BC的中线,
∴S△ABD=S△ACD,
∵DE,DF分别是△ABD和△ACD的高,
∴S△ABD=$\frac{1}{2}$AB•DE,S△ACD=$\frac{1}{2}$AC•DF,
∴AB•DE=AC•DF,
∴$\frac{DE}{DF}$=$\frac{AC}{AB}$=$\frac{4}{3}$.
点评 本题考查了三角形的面积,三角形的直线把三角形分成面积相等的两个三角形是解题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
14.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
| A. | -3.5 | B. | +2.5  | C. | -0.6  | D. | +0.7  |
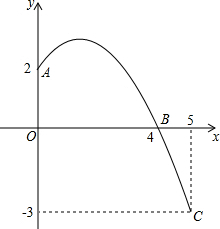 已知:如图是抛物线y=ax2+bx+c(a≠0)的一部分,且图象经过A,B,C三点,求抛物线的解析式.
已知:如图是抛物线y=ax2+bx+c(a≠0)的一部分,且图象经过A,B,C三点,求抛物线的解析式. 如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证:
如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证: 敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?
敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?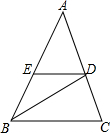 如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.
如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由. 如图,EF∥CD,EF∥AB,求证:EM=FN.
如图,EF∥CD,EF∥AB,求证:EM=FN.