题目内容
1.某次数学竞赛,初一(1)班9名参赛同学的成绩(单位:分)分别为85,84,95,x,y,93,78,95,110,若这9名同学成绩的唯一众数为85分,平均成绩为90分,y为中位数,试求x,y的值.分析 根据众数的定义得出x、y中至少有一个数为85,假设x为85,根据平均数的计算公式求出y,再根据y为中位数,得出假设不成立,再假设y=85,求出x的值,再根据题意进行验证,即可得出正确答案.
解答 解:因为这9名同学成绩的唯一众数为85分,
所以x、y中至少有一个数为85,
假设x为85,
又因为平均成绩为90分,
所以$\frac{1}{9}$×(85+84+95+85+y+93+78+95+110)=90.
解得:y=85.
但85是这列数的中位数,符合题意;
假设y=85,
又因为平均成绩为90分,
所以$\frac{1}{9}$×(85+84+95+x+85+93+78+95+110)=90.
解得:x=85.
符合题意,
所以x=85,y=85.
点评 此题考查了众数和中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会错误地将这组数据最中间的那个数当作中位数;众数是一组数据中出现次数最多的数.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.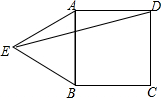 如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
 如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )| A. | $\sqrt{23}$ | B. | 2$\sqrt{10}$ | C. | $\sqrt{41}$ | D. | 5$\sqrt{2}$ |
16.下列整式计算正确的是( )
| A. | (2a)3=6a3 | B. | x4÷x4=x | C. | x2•x3=x5 | D. | (m3)3=m6 |
12.下列各式中,同学们的计算结果不正确的是( )
| A. | $\sqrt{5}×\sqrt{7}$=2$\sqrt{3}$ | B. | $\sqrt{6}÷\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{\frac{1}{10}}$×$\sqrt{8}$=$\frac{2\sqrt{5}}{5}$ | D. | $\sqrt{\frac{4}{7}}$÷$\sqrt{\frac{7}{4}}$=$\frac{4}{7}$ |
9.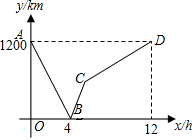 如图所示,一列列车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km)图中的折线表示y与x之间的函数关系,下列说法中错误的是( )
如图所示,一列列车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km)图中的折线表示y与x之间的函数关系,下列说法中错误的是( )
 如图所示,一列列车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km)图中的折线表示y与x之间的函数关系,下列说法中错误的是( )
如图所示,一列列车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km)图中的折线表示y与x之间的函数关系,下列说法中错误的是( )| A. | B点表示快车与慢车出发4小时两车相遇 | |
| B. | B-C-D段表示慢车先加速后减速最后到达甲地 | |
| C. | 快车的速度为200km/h | |
| D. | 慢车的速度为100km/h |
 如图,在四边形ABCD中,AD∥BC,要使△ABD≌△CDB,可添加一个条件为∠A=∠C.
如图,在四边形ABCD中,AD∥BC,要使△ABD≌△CDB,可添加一个条件为∠A=∠C.