题目内容
9.计算:(1)(3a+$\frac{1}{4}$b2)($\frac{1}{4}$b2-3a)
(2)(m-2n)2
(3)(a-3b-3)(a-3b+3)
分析 (1)利用平方差公式展开即可;
(2)利用完全平方公式展开即可;
(3)先利用平方差公式计算得到原式=(a-3b)2-9,然后利用完全平方公式展开即可.
解答 解:(1)原式=($\frac{1}{4}$b2)2-(3a)2
=$\frac{1}{16}$b4-9a2;
(2)原式=m2-4mn+4n2;
(3)原式=(a-3b)2-9
=a2-6ab+9b2-9.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
相关题目
1.某次数学竞赛,初一(1)班9名参赛同学的成绩(单位:分)分别为85,84,95,x,y,93,78,95,110,若这9名同学成绩的唯一众数为85分,平均成绩为90分,y为中位数,试求x,y的值.
4.下列各式正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{-8}$=-2 | C. | $\sqrt{{3}^{2}+{4}^{2}}$=7 | D. | 以上都不对 |
14. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )| A. | 4.6 | B. | 4.8 | C. | 5 | D. | 5.2 |
16.若等腰三角形的一边是9,另一边是5,则此等腰三角形的周长是( )
| A. | 23 | B. | 19 | C. | 19或23 | D. | 无法确定 |
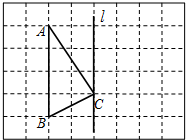 如图,在正方形网格中,△ABC的三个顶点都在方格图的格点上.请画出△A'B'C',使△A'B'C'和△ABC关于直线l成轴对称.
如图,在正方形网格中,△ABC的三个顶点都在方格图的格点上.请画出△A'B'C',使△A'B'C'和△ABC关于直线l成轴对称.