题目内容
19.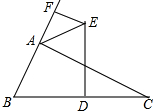 如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.
如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.
分析 过E作EN⊥AC于N,并连接EB、EC,可证得△FAE≌△NAE,进一步可证得△EFB≌△ENC,可得到AC=2AF+AB,可求得AC的长.
解答 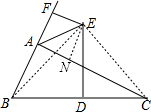 解:过E作EN⊥AC于N,并连接EB、EC.
解:过E作EN⊥AC于N,并连接EB、EC.
∵EA平分∠FAC,
∴∠EAF=∠EAN,
∵EF⊥AB,EN⊥AC,
∴∠EFA=∠ENA=90°,
在△FAE和△NAE中,
$\left\{\begin{array}{l}{∠EFA=∠ENA}\\{∠EAF=∠EAN}\\{AE=AE}\end{array}\right.$,
∴△FAE≌△NAE(AAS),
∴EF=EN,AF=AN,
∵DE垂直平分BC,
∴EB=EC,
在Rt△EFB和Rt△ENC中,
$\left\{\begin{array}{l}{EF=EN}\\{EB=EC}\end{array}\right.$,
∴Rt△EFB≌Rt△ENC(HL),
∴FB=NC,
∴AC=AN+NC=AF+BF=2AF+AB=6+7=13,
故答案为:13.
点评 本题主要考查线段垂直平分线的性质和全等三角形的判定和性质,通过证明三角形全等得出AC=2AF+AB是解题的关键.

练习册系列答案
相关题目
9.等腰三角形的底角为80°,则它的顶角是( )
| A. | 80° | B. | 60° | C. | 40° | D. | 20° |
10.反比例函数$y=-\frac{2}{x}$图象上有三点$A(-\frac{1}{2},{y_1})$、B(-1,y2)、$B(\frac{1}{3},{y_3})$,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
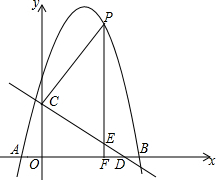 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m. 如图,AB=AC,DC=DB,∠A+∠D=180°,求证:∠B=∠C=90°.
如图,AB=AC,DC=DB,∠A+∠D=180°,求证:∠B=∠C=90°.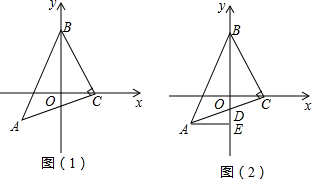
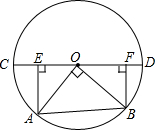 如图,CD为⊙O的直径,OA,OB是⊙O的半径,OA⊥OB,作AE⊥CD于E,BF⊥CD于F,已知AB=5$\sqrt{2}$.求CE+AE+BF+DF的值.
如图,CD为⊙O的直径,OA,OB是⊙O的半径,OA⊥OB,作AE⊥CD于E,BF⊥CD于F,已知AB=5$\sqrt{2}$.求CE+AE+BF+DF的值.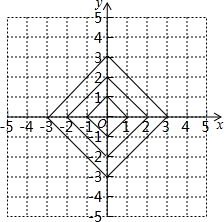 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.