题目内容
7.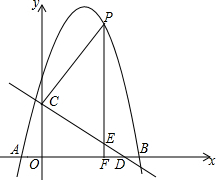 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;
(2)若PE=5EF,求m的值.
分析 (1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解.
解答 解:(1)将点A、B坐标代入抛物线解析式,得:
$\left\{\begin{array}{l}{-1-b+c=0}\\{-25+5b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{c=5}\end{array}\right.$.
故抛物线的解析式为:y=-x2+4x+5;
(2)∵点P的横坐标为m,
∴P(m,-m2+4m+5),E(m,-$\frac{3}{4}$m+3),F(m,0).
∴PE=|yP-yE|=|(-m2+4m+5)-(-$\frac{3}{4}$m+3)|=|-m2+$\frac{19}{4}$m+2|,
EF=|yE-yF|=|(-$\frac{3}{4}$m+3)-0|=|-$\frac{3}{4}$m+3|.
由题意,PE=5EF,即:|-m2+$\frac{19}{4}$m+2|=5|-$\frac{3}{4}$m+3|=|-$\frac{15}{4}$m+15|
①若-m2+$\frac{19}{4}$m+2=-$\frac{15}{4}$m+15,
整理得:2m2-17m+26=0,
解得:m1=2,m2=$\frac{13}{2}$;
②若-m2+$\frac{19}{4}$m+2=-(-$\frac{15}{4}$m+15),
整理得:m2-m-17=0,
解得:m=$\frac{1+\sqrt{69}}{2}$或m=$\frac{1-\sqrt{69}}{2}$.
由题意得,m的取值范围为:-1<m<5,
故m=$\frac{13}{2}$、m=$\frac{1-\sqrt{69}}{2}$这两个解均舍去.
∴m=2或m=$\frac{1+\sqrt{69}}{2}$.
点评 本题考查了二次函数与一次函数的图象与性质、点的坐标、待定系数法求函数解析式等多个知识点,需要注意的是,为了避免漏解,表示线段长度的代数式均含有绝对值,解方程时需要分类讨论、分别计算.

| A. | 对顶角 | B. | 相等但不是对顶角 | ||
| C. | 邻补角 | D. | 互补但不是邻补角 |
 如图:两个同心圆,其中大圆的弦AD交小圆于C、D两点那么:AB与CD相等吗?为什么?
如图:两个同心圆,其中大圆的弦AD交小圆于C、D两点那么:AB与CD相等吗?为什么?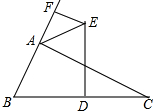 如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.
如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13. 如图,直线l交线段AB于点P,AC⊥l,BD⊥l,垂足分别为C、D,M是AB的中点,求证:MC=MD.
如图,直线l交线段AB于点P,AC⊥l,BD⊥l,垂足分别为C、D,M是AB的中点,求证:MC=MD. 如图,⊙O1与⊙O2交于A、B两点,P是⊙O1上的点,连接PA、PB交⊙O2于C、D,求证:PO1⊥CD.
如图,⊙O1与⊙O2交于A、B两点,P是⊙O1上的点,连接PA、PB交⊙O2于C、D,求证:PO1⊥CD.