题目内容
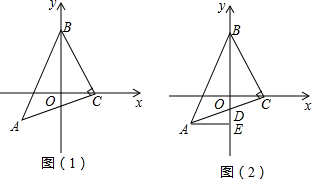
2.如图,△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,以锐角顶点B在y轴上.(1)如图(1)若点C的坐标是(2,0),点A的坐标是(-2,-2),求B点的坐标.
(2)如图(2),若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,问BD与AE之间有怎样的数量关系,并说明理由.
分析 (1)过点A作AD⊥OC,可证△ADC≌△COB,根据全等三角形对应边相等即可解题;
(2)延长BC,AE交于点F,可证△ACF≌△BCD,可证△ABE≌△FBE,即可求得BD=2AE.
解答 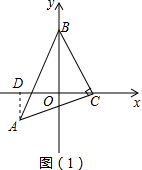 解:(1)如图(1)过点A作AD⊥x轴于D,
解:(1)如图(1)过点A作AD⊥x轴于D,
∵∠DAC+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠BCD=∠DAC,
在△ADC和△COB中,
$\left\{\begin{array}{l}{∠ADC=∠BOC=90°}\\{∠DAC=∠BCD}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△COB(AAS),
∴AD=OC,CD=OB,
∴点B坐标为(0,4);
(2)如图(2)延长BC,AE交于点F,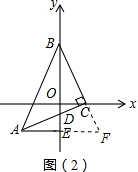 ∵AC=BC,AC⊥BC,
∵AC=BC,AC⊥BC,
∴∠BAC=∠ABC=45°,
∵BD平分∠ABC,
∴∠COD=22.5°,∠DAE=90°-∠ABD-∠BAD=22.5°,
在△ACF和△BCD中,
$\left\{\begin{array}{l}{∠DAE=∠COD}\\{BC=AC}\\{∠BCD=∠ACF=90°}\end{array}\right.$,
∴△ACF≌△BCD(ASA),
∴AF=BD,
在△ABE和△FBE中,
$\left\{\begin{array}{l}{∠ABE=∠FBE}\\{BE=BE}\\{∠AEB=∠FEB}\end{array}\right.$,
∴△ABE≌△FBE(ASA),
∴AE=EF,
∴BD=2AE.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,坐标与图形的性质,思路掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.若a是有理数,则下列判断正确的是( )
| A. | |a|是正数 | B. | -a是负数 | C. | |a|是正数或0 | D. | |-a|是负数或0 |
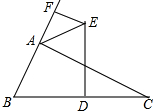 如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.
如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.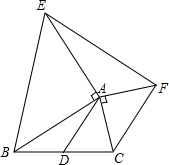 已知,如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形(其中∠BAE=∠CAF=90°,AE=AB,AC=AF),求证:EF=2AD.
已知,如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形(其中∠BAE=∠CAF=90°,AE=AB,AC=AF),求证:EF=2AD. 如图,直线l交线段AB于点P,AC⊥l,BD⊥l,垂足分别为C、D,M是AB的中点,求证:MC=MD.
如图,直线l交线段AB于点P,AC⊥l,BD⊥l,垂足分别为C、D,M是AB的中点,求证:MC=MD.