题目内容
2.图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:
(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,则∠ABX+∠ACX=40°;
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4,若∠BDC=135°,∠BG1C=67°,求∠A的度数.
分析 (1)连接AD并延长,根据三角形的外角和内角关系解答;
(2)①利用(1)的结论,直接计算出∠ABX+∠ACX的度数;
②图(3)利用(1)的结论,根据∠BDC=135°,∠BG1C=67°,计算出相等的角:∠DBG4+∠DCG4的和,再次利用(1)的结论,求出∠A的度数.
解答 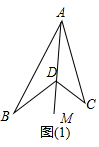 解:(1)∠BDC=∠A+∠B+∠C.理由:
解:(1)∠BDC=∠A+∠B+∠C.理由:
连接AD并延长到M.
因为∠BDM=∠BAD+∠B,∠CDM=∠CAD+∠C,
所以∠BDM+∠CDM=∠BAD+∠B+∠CAD+∠C,
即∠BDC=∠BAC+∠B+∠C.
(2)①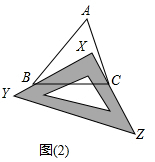 由(1)知:∠BXC=∠A+∠ABX+∠ACX,
由(1)知:∠BXC=∠A+∠ABX+∠ACX,
由于∠BXC=90°,∠A=50°
所以∠ABX+∠ACX
=∠BXC-∠A
=90°-50°
=40°.
②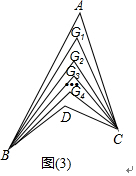 在箭头图G1BDC中
在箭头图G1BDC中
因为∠BDC=∠G1+∠G1BD+∠G1CD,
又∵∠BDC=135°,∠BG1C=67°
∵∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4
∴4(∠DBG4+∠DCG4)=135°-67°
∴∠DBG4+∠DCG4=17°.
∴∠ABG1+∠ACG1=17°
∵在箭头图G1BAC中
∵∠BG1C=∠A+∠G1BA+∠G1CA,
又∵∠BG1C=67°,
∴∠A=50°.
答:∠A的度数是50°.
点评 本题考查了外角和内角的关系以及角的计算.找出“箭头图”并利用“箭头图”间角的关系是解决本题的关键

练习册系列答案
相关题目
12.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为720元,按标价的五折销售,仍可获利20%,则这件商品的进价为( )
| A. | 200元 | B. | 144元 | C. | 300元 | D. | 360元 |
13.下列函数中,y是x的二次函数的是( )
| A. | y=2x-1 | B. | y=-$\frac{1}{x}$ | C. | y=x-x2 | D. | y=$\frac{1}{{x}^{2}}$+x |
17.使分式$\frac{x}{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≠0 | C. | x≠-1 | D. | x≠0且x≠1. |
7.已知(m-n)2=34,(m+n)2=4 000,则m2+n2的值为( )
| A. | 2 016 | B. | 2 017 | C. | 2 018 | D. | 4 034 |
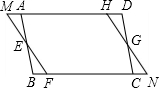 如图四边形ABCD、MFNH都是平行四边形,MAHD和BFCN都在一直线上,HD=FB.
如图四边形ABCD、MFNH都是平行四边形,MAHD和BFCN都在一直线上,HD=FB.
 如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?