题目内容
15.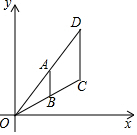 如图,在平面直角坐标系中,点A在△ODC的OD边上,AB∥DC交OC于点B.若点A、B的坐标分别为(2,3)、(2,1),点C的横坐标为2m(m>0),则点D的坐标为( )
如图,在平面直角坐标系中,点A在△ODC的OD边上,AB∥DC交OC于点B.若点A、B的坐标分别为(2,3)、(2,1),点C的横坐标为2m(m>0),则点D的坐标为( )| A. | (2m,m) | B. | (2m,2m) | C. | (2m,3m) | D. | (2m,4m) |
分析 先判定△OAB和△ODC是以原点为位似中心的位似图形,然后利用B、C的横坐标的规律得到相似比为m,然后把A点的横纵坐标都乘以m即可得到D点坐标.
解答 解:∵AB∥CD,
∴△OAB和△ODC是以原点为位似中心的位似图形,
而B(2,1),C点的横坐标为2m,
∴把A点的纵坐标乘以m可得D点的纵坐标,
即点D的横坐标为(2m,3m).
故选C.
点评 本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
相关题目
7.已知(m-n)2=34,(m+n)2=4 000,则m2+n2的值为( )
| A. | 2 016 | B. | 2 017 | C. | 2 018 | D. | 4 034 |
3.如图所示的操作步骤,若输入x的值为5,则输出的值为( )


| A. | 94 | B. | 95 | C. | 96 | D. | 97 |
 如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?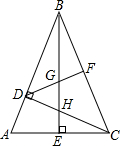 如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE
如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE