题目内容
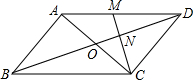 如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
考点:相似三角形的判定与性质,平行四边形的性质
专题:几何综合题
分析:(1)由四边形ABCD为平行四边形,得到对边平行且相等,且对角线互相平分,根据两直线平行内错角相等得到两对角相等,进而确定出三角形MND与三角形CNB相似,由相似得比例,得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;
(2)由相似三角形相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND,最后由S四边形ABNM=S△ABD-S△MND求解.
(2)由相似三角形相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND,最后由S四边形ABNM=S△ABD-S△MND求解.
解答:解:(1)∵平行四边形ABCD,
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴
=
,
∵M为AD中点,
∴MD=
AD=
BC,即
=
,
∴
=
,即BN=2DN,
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6;
(2)∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=DN:BN=1:2,
∴S△MND=
S△CND=1,S△BNC=2S△CND=4.
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴
| MD |
| CB |
| DN |
| BN |
∵M为AD中点,
∴MD=
| 1 |
| 2 |
| 1 |
| 2 |
| MD |
| CB |
| 1 |
| 2 |
∴
| DN |
| BN |
| 1 |
| 2 |
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6;
(2)∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=DN:BN=1:2,
∴S△MND=
| 1 |
| 2 |
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
点评:此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
若abc>0,则
+
+
的值为( )
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
| A、2 | B、-2 |
| C、2或-2 | D、以上都不对 |
 时,每个元件的状态有两种可能:通过或断开,并且这两种状态的可能性相等.
时,每个元件的状态有两种可能:通过或断开,并且这两种状态的可能性相等.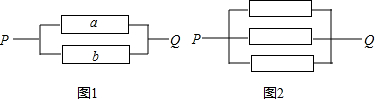
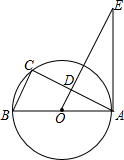 如图,AB为圆O的直径,点C在圆O上,过点O作BC的平行线交AC于点D,交过点A的直线于点E,且∠E=∠BAC.
如图,AB为圆O的直径,点C在圆O上,过点O作BC的平行线交AC于点D,交过点A的直线于点E,且∠E=∠BAC.