题目内容
1. 如图,在等边三角形ABC中,点D在BC上,以AD为一边作等边三角形ADE,连接EB.
如图,在等边三角形ABC中,点D在BC上,以AD为一边作等边三角形ADE,连接EB.(1)求证:∠CAD=∠BAE;
(2)求:∠ABE的度数.
分析 (1)利用等边三角形的性质,可求得∠BAC=∠DAE=60°,再利用角的和差可证明结论;
(2)由条件可证明可△CAD≌△BAE,可求得∠ABE=∠C,可求得答案.
解答 (1)证明:
∵△ABC和△ADE为等边三角形,
∴∠EAD=∠BAC=60°,
∴∠BAC-∠BAD=∠DAE-∠BAD,
∴∠CAD=∠BAE;
(2)解:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AD=AE,∠C=60°,
在△ACD和△ABE中
$\left\{\begin{array}{l}{AB=AC}\\{∠CAD=∠BAE}\\{AD=AE}\end{array}\right.$
∴△ACD≌△ABE(SAS),
∴∠ABE=∠C=60°.
点评 本题主要考查等边三角形的性质及全等三角形的判定方法和性质,掌握等边三角形的三条边相等、三个角也相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
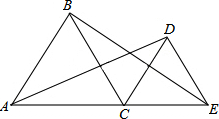 如图,已知C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,连接AD,BE,AC=5,AD=7,则BE=7.
如图,已知C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,连接AD,BE,AC=5,AD=7,则BE=7.