题目内容
12.某检修小组1乘一辆汽车沿公路检修线路,约定向东为正,某天从A地出发到收工时,行走记录为(单位:千米):+15,-4,+5,-1,+8,-3.另一小组2也从A地出发,在南北向修,约定向北为正,行走记录为(单位:千米):-17,+12,+6,-5,+8,-6.(1)分别计算收工时,1,2两组在A地的哪一边,距A地多远?;
(2)求两个检修小组各走了多少千米;
(3)若检修车毎千米耗油3.5升,求从出发到收工两个检修小组共耗油多少升?.
分析 (1)把每个小组记录的数字相加,根据计算的结果和题中规定的正方向即可确定出收工时两组在甲地的哪一边以及距甲地的距离;
(2)把各组记录的数字的绝对值相加即可得到各组在检修过程中总共行进的距离;
(3)根据每千米汽车耗油量为3.5升,把行进的总距离乘以3.5即可得到各小组的耗油量.
解答 解:(1)根据题意得:15-4+5-1+8-3=20,
∴1组在甲地的东边,距A地39千米,
根据题意得:-17+12+6-5+8-6=-2,
∴2组在甲地的南边,距A地2千米;
(2)根据题意得:1组:|15|+|-4|+|5|+|-1|+|8|+|-3|=36千米;
2组:|-17|+|12|+|6|+|-5|+|8|+|-6|=54千米;
3、(36+54)×3.5=31.5升,
所以从出发到收工两个检修小组共耗油31.5升.
点评 此题考查了正数和负数,以及有理数加减法的应用,弄清题意是解本题的关键.

练习册系列答案
相关题目
2.已知Rt△ABC中,a、b为直角边,c为斜边,h为斜边上的高,则下面说法错误的是( )
| A. | ab=ch | |
| B. | h<a | |
| C. | 以ah、bh、ab为边的三角形是直角三角形 | |
| D. | 以a+b、ab、c为边的三角形是直角三角形 |
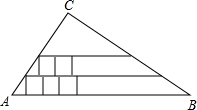 如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.
如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.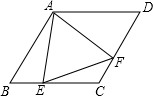 如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=24°,求∠CEF的度数.
如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=24°,求∠CEF的度数. 如图,在等边三角形ABC中,点D在BC上,以AD为一边作等边三角形ADE,连接EB.
如图,在等边三角形ABC中,点D在BC上,以AD为一边作等边三角形ADE,连接EB.