题目内容
10．已知$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$是二元一次方程mx+2y=-4的解，则m的值是3．分析 根据$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$是二元一次方程mx+2y=-4的解，可以求得m的值，本题得以解决．
解答 解：∵$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$是二元一次方程mx+2y=-4的解，
∴m×（-2）+2×1=-4，
解得，m=3，
故答案为：3．
点评 本题考查二元一次方程的解，解题的关键是明确题意，求出相应的m的值．
练习册系列答案
相关题目
20．
某工厂投入生产一种机器，当该机器生产数量至少10台，但不超过70台，每台成本y与生产数量x之间是一次函数关系，函数y与自变量x的部分对应值如表：
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
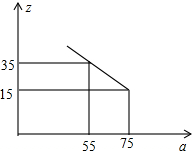
（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元∕台）之间满足如图所示的函数关系，求z与a之间的函数关系式．
（3）若该厂第一个月生产这种机器50台，且第一个月按同一售价共卖出这种机器25台，请你求出该厂第一个月销售这种机器的利润．（注：利润=售价-成本）
某工厂投入生产一种机器，当该机器生产数量至少10台，但不超过70台，每台成本y与生产数量x之间是一次函数关系，函数y与自变量x的部分对应值如表：| x（单位：台） | 10 | 20 | 30 |
| y（单位：万元∕台） | 60 | 55 | 50 |
（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元∕台）之间满足如图所示的函数关系，求z与a之间的函数关系式．
（3）若该厂第一个月生产这种机器50台，且第一个月按同一售价共卖出这种机器25台，请你求出该厂第一个月销售这种机器的利润．（注：利润=售价-成本）
1．已知一次函数y=kx+b的图象经过（1，a）和（a，-1），其中a＞1，则k，b的取值范围是（ ）
| A． | k＞0，b＞0 | B． | k＜0，b＞0 | C． | k＞0，b＜0 | D． | k＜0，b＜0 |
18．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC2=PE•PO．
2．下列图形既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．
如图，直线AB和CD相交于点O，若∠AOD=134°，则∠AOC的度数为（ ）
如图，直线AB和CD相交于点O，若∠AOD=134°，则∠AOC的度数为（ ）| A． | 134° | B． | 144° | C． | 46° | D． | 32° |