题目内容
10.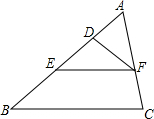 如图,在△ABC中,D,E在AB上,EF∥BC,EF交AC于点F,∠ADF=∠C,△ABC∽△AFD.若AF=6cm,CF=AD=4cm,求AB和AE的长.
如图,在△ABC中,D,E在AB上,EF∥BC,EF交AC于点F,∠ADF=∠C,△ABC∽△AFD.若AF=6cm,CF=AD=4cm,求AB和AE的长.
分析 根据△ABC∽△AFD,得到$\frac{AD}{AC}=\frac{AF}{AB}$,代入已知条件即可得到AB的值,根据EF∥BC,得到比例式,解方程即可得到结果.
解答 解:∵△ABC∽△AFD,
∴$\frac{AD}{AC}=\frac{AF}{AB}$,
即$\frac{4}{10}=\frac{6}{AB}$,
∴AB=15,
∵EF∥BC,
∴$\frac{AE}{AB}=\frac{AF}{AC}$,
即$\frac{AE}{15}=\frac{6}{10}$,
∴AE=9.
点评 本题考查了相似三角形的性质和判定,平行线分线段成比例,熟练掌握相似三角形的性质和判定是解题的关键.

练习册系列答案
相关题目
20.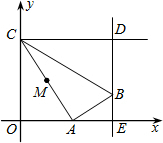 如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
 如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )| A. | 2或2+3$\sqrt{2}$ | B. | 2或2+3$\sqrt{3}$ | C. | 3或3+5$\sqrt{3}$ | D. | 3或3+5$\sqrt{2}$ |
5. 如图,若△ABC∽△DEF,则∠D的度数为( )
如图,若△ABC∽△DEF,则∠D的度数为( )
 如图,若△ABC∽△DEF,则∠D的度数为( )
如图,若△ABC∽△DEF,则∠D的度数为( )| A. | 30° | B. | 50° | C. | 100° | D. | 以上都不对 |
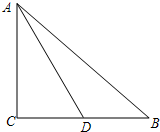 如图,在△ABC中,∠C=90°,AC=BC=10,点D是BC的中点,以直线AD为折痕,将△ABD翻折到△AB′D处,BB′与直线AD相交于点E,则线段AE的长为6$\sqrt{5}$.
如图,在△ABC中,∠C=90°,AC=BC=10,点D是BC的中点,以直线AD为折痕,将△ABD翻折到△AB′D处,BB′与直线AD相交于点E,则线段AE的长为6$\sqrt{5}$.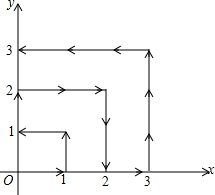 如图,在平面直角坐标系的第一象限内,如果原点是1号点,(1,0)点是2号点,(1,1)点是3号点,(0,1)点是4号点,(0,2)点是5号点,…按箭头所示,第2008号点的坐标是(0,669).
如图,在平面直角坐标系的第一象限内,如果原点是1号点,(1,0)点是2号点,(1,1)点是3号点,(0,1)点是4号点,(0,2)点是5号点,…按箭头所示,第2008号点的坐标是(0,669).