题目内容
1.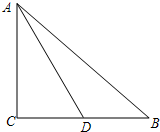 如图,在△ABC中,∠C=90°,AC=BC=10,点D是BC的中点,以直线AD为折痕,将△ABD翻折到△AB′D处,BB′与直线AD相交于点E,则线段AE的长为6$\sqrt{5}$.
如图,在△ABC中,∠C=90°,AC=BC=10,点D是BC的中点,以直线AD为折痕,将△ABD翻折到△AB′D处,BB′与直线AD相交于点E,则线段AE的长为6$\sqrt{5}$.
分析 由在Rt△ABC中,∠C=90°,AC=BC=10,于是得到AD,又由△ADB沿直线AD翻折后,将点B落在点B′处,于是得到AB=AB′∠BAD=∠B′AD,根据等腰三角形的性得到AE⊥B′B,求得△ACD∽△BDE,证得$\frac{CD}{DE}=\frac{AD}{BD}$,于是得到DE=$\sqrt{5}$,即可得到结论.
解答 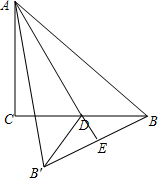 解:在△ABC中,∠C=90°,AC=BC=10,点D是BC的中点,
解:在△ABC中,∠C=90°,AC=BC=10,点D是BC的中点,
∴BD=CD=5,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=5$\sqrt{5}$,
∵将△ABD翻折到△AB′D处,
∴AB=AB′∠BAD=∠B′AD,
∴AE⊥B′B,
∵∠ADC=∠BDE,
∴△ACD∽△BDE,
∴$\frac{CD}{DE}=\frac{AD}{BD}$,
∴$\frac{5}{DE}=\frac{5\sqrt{5}}{5}$,
∴DE=$\sqrt{5}$,
∴AE=AD+DE=6$\sqrt{5}$.
故答案为:6$\sqrt{5}$.
点评 此题考查了折叠的性质、直角三角形的性质以及等腰直角三角形性质.此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系.

练习册系列答案
相关题目
16. 如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
 如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
6.关于三角形内角的叙述错误的是( )
| A. | 三角形三个内角的和是180° | |
| B. | 三角形两个内角的和一定大于60° | |
| C. | 三角形中至少有一个角不小于60° | |
| D. | 一个三角形中最大的角所对的边最长 |
 如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为$\frac{5}{2}$.
如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为$\frac{5}{2}$.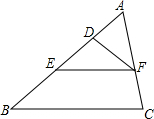 如图,在△ABC中,D,E在AB上,EF∥BC,EF交AC于点F,∠ADF=∠C,△ABC∽△AFD.若AF=6cm,CF=AD=4cm,求AB和AE的长.
如图,在△ABC中,D,E在AB上,EF∥BC,EF交AC于点F,∠ADF=∠C,△ABC∽△AFD.若AF=6cm,CF=AD=4cm,求AB和AE的长. 如图所示,点A,B,C在同一直线上,点M在AC外,经过图中的三个点作圆,可以作3个.
如图所示,点A,B,C在同一直线上,点M在AC外,经过图中的三个点作圆,可以作3个.