题目内容
20.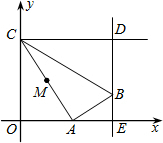 如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )| A. | 2或2+3$\sqrt{2}$ | B. | 2或2+3$\sqrt{3}$ | C. | 3或3+5$\sqrt{3}$ | D. | 3或3+5$\sqrt{2}$ |
分析 先证明△CAO∽△ABE,得出对应边成比例,得出BE=$\frac{1}{2}$t,AE=2.分两种情况:
①当0<t<8时;根据题意得出方程,解方程即可;
②当t>8时;根据题意得出方程,解方程即可.
解答 解:根据题意得:∠BAC=90°,
∴∠CAO+∠BAE=90°,
∵BE⊥x轴,
∴∠AEB=90°=∠AOC,
∴∠ABE+∠BAE=90°,
∴∠CAO=∠ABE.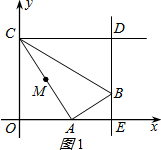
∴△CAO∽△ABE.
∴$\frac{CA}{AB}=\frac{AO}{BE}$=$\frac{OC}{AE}$,
∵M是AC的中点,AB=AM,
∴CA=2AB,
∴$\frac{2AB}{AB}=\frac{t}{BE}$=$\frac{4}{AE}$,
∴BE=$\frac{1}{2}$t,AE=2.
分两种情况:
①当0<t<8时,如图1所示:
S=$\frac{1}{2}$CD•BD=$\frac{1}{2}$(2+t)(4-$\frac{t}{2}$)=$\frac{25}{4}$.
解得:t1=t2=3.
②当t>8时,如图2所示: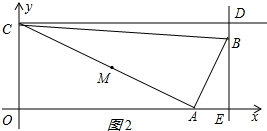
S=$\frac{1}{2}$CD•BD=$\frac{1}{2}$(2+t)( $\frac{t}{2}$-4)=$\frac{25}{4}$.
解得:t1=3+5$\sqrt{2}$,t2=3-5$\sqrt{2}$(不合题意,舍去).
综上所述:当t=3或3+5$\sqrt{2}$时,S=$\frac{25}{4}$;
故选:D.
点评 本题是一次函数综合题目,考查了相似三角形的判定与性质、角的互余关系、三角形面积的计算方法、解方程等知识;本题综合性强,有一定难度,需要进行分类讨论才能得出结果.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若BP=3,求PP′的长.
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若BP=3,求PP′的长. 已知抛物线y=ax2+bx+2经过点A(-2、0)、C($\frac{3}{2}$,0),与y轴交于点B.动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交于y轴于点Q.设点P的运动时间为t秒.
已知抛物线y=ax2+bx+2经过点A(-2、0)、C($\frac{3}{2}$,0),与y轴交于点B.动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交于y轴于点Q.设点P的运动时间为t秒.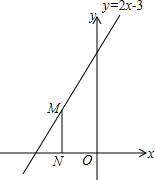 如图,点M是直线y=2x+3上的动点,过点M作MH⊥x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形?小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,△MNP为等腰直角三角形,请你写出y轴上其它M在x轴上方点P的坐标(0,0),(0,$\frac{3}{4}$),(0,1).
如图,点M是直线y=2x+3上的动点,过点M作MH⊥x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形?小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,△MNP为等腰直角三角形,请你写出y轴上其它M在x轴上方点P的坐标(0,0),(0,$\frac{3}{4}$),(0,1). 如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为$\frac{5}{2}$.
如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为$\frac{5}{2}$.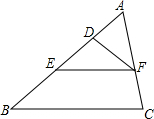 如图,在△ABC中,D,E在AB上,EF∥BC,EF交AC于点F,∠ADF=∠C,△ABC∽△AFD.若AF=6cm,CF=AD=4cm,求AB和AE的长.
如图,在△ABC中,D,E在AB上,EF∥BC,EF交AC于点F,∠ADF=∠C,△ABC∽△AFD.若AF=6cm,CF=AD=4cm,求AB和AE的长.