题目内容
(1)计算:
•(
÷
);
(2)已知实数x、y满足:
+(y-
)2=0,求
的值.
|
|
| b |
(2)已知实数x、y满足:
| 2x+y |
| 1 |
| 2 |
| x+y |
考点:二次根式的乘除法,非负数的性质:偶次方,非负数的性质:算术平方根
专题:计算题
分析:(1)利用二次根式的乘除法法则求解;
(2)利用算术平方根和一个数的平方等于0求出x,y,再求
的值.
(2)利用算术平方根和一个数的平方等于0求出x,y,再求
| x+y |
解答:解:(1)
•(
÷
)
=
•
=
=
=
;
(2)由
+(y-
)2=0,
可知,
=0且(y-
)2=0,
即
,
解得
.
所以
=
=
.
|
|
| b |
=
|
|
=
|
=
|
=
| ||
| b |
(2)由
| 2x+y |
| 1 |
| 2 |
可知,
| 2x+y |
| 1 |
| 2 |
即
|
解得
|
所以
| x+y |
-
|
| 1 |
| 2 |
点评:本题主要考查了二次根式的乘除法,非负数的性质及算术平方根,解题的关键是利用算术平方根和一个数的平方等于0求解.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
计算2
-5
的结果是( )
| 7 |
| 7 |
A、3
| ||
B、2
| ||
C、-3
| ||
D、-2
|
如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有( )


| A、2种 | B、3种 | C、4种 | D、5种 |
已知正六边形的面积为6
,则其边长为( )
| 3 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、2
|
若9a2+6(k-3)a+1是完全平方式,则k的值是( )
| A、±4 | B、±2 | C、3 | D、4或2 |
 已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.
已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF. 以点A(0,4),B(8,4),C(0,8)为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.
以点A(0,4),B(8,4),C(0,8)为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.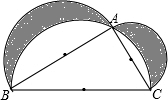 如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.