题目内容
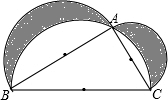 如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.考点:勾股定理
专题:
分析:分别求出以AB、AC、BC为直径的半圆及△ABC的面积,再根据S阴影=S1+S2+S△ABC-S3即可得出结论.
解答:解:∵∠BAC=90°,AB=4cm,AC=3cm,BC=5cm,
∴以AB为直径的半圆的面积S1=2π(cm2);
以AC为直径的半圆的面积S2=
π(cm2);
以BC为直径的半圆的面积S3=
π(cm2);
S△ABC=6(cm2);
∴S阴影=S1+S2+S△ABC-S3=6(cm2).
∴以AB为直径的半圆的面积S1=2π(cm2);
以AC为直径的半圆的面积S2=
| 9 |
| 8 |
以BC为直径的半圆的面积S3=
| 25 |
| 8 |
S△ABC=6(cm2);
∴S阴影=S1+S2+S△ABC-S3=6(cm2).
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=
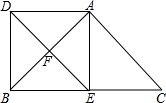 如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.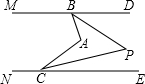 如图,已知,∠MBA+∠BAC+∠NCA=360°,
如图,已知,∠MBA+∠BAC+∠NCA=360°, 如图,平行四边形ABCD的对角线AC、BD交于一点O,AB=11,△OCD的周长为27,则AC+BD=
如图,平行四边形ABCD的对角线AC、BD交于一点O,AB=11,△OCD的周长为27,则AC+BD=