题目内容
如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有( )


| A、2种 | B、3种 | C、4种 | D、5种 |
考点:一元一次方程的应用
专题:
分析:可设折痕对应的刻度为xcm,根据折叠的性质和三段长度由短到长的比为1:2:3,长为60cm的卷尺,列出方程求解即可.
解答:解:设折痕对应的刻度为xcm,依题意有
①x+x+x=60,
解得x=20;
②x+x+0.4x=60,
解得x=25;
③x+x-
x=60,
解得x=35;
④x+x-
x=60,
解得x=40.
综上所述,折痕对应的刻度有4种可能.
故选:C.
①x+x+x=60,
解得x=20;
②x+x+0.4x=60,
解得x=25;
③x+x-
| 2 |
| 7 |
解得x=35;
④x+x-
| 1 |
| 2 |
解得x=40.
综上所述,折痕对应的刻度有4种可能.
故选:C.
点评:考查了一元一次方程的应用和图形的剪拼,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.注意分类思想的运用.

练习册系列答案
相关题目
下列表述能确定位置的是( )
| A、电影院2排 |
| B、学校教学楼北 |
| C、北偏东30° |
| D、东经117°,北纬42° |
下列说法中,错误的是( )
| A、“同位角相等”是命题 |
| B、证明假命题,只要举一个反例即可 |
| C、命题是判断一件事情的句子 |
| D、任意两个正方形都是位似图形 |
 如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC长的2倍,则△ABC纸片扫过的面积为( )
如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC长的2倍,则△ABC纸片扫过的面积为( )| A、18cm2 |
| B、21cm2 |
| C、27cm2 |
| D、30cm2 |
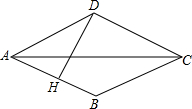 如图,菱形ABCD的边长为15cm,对角线AC=24cm,DH⊥AB于H,则DH的长为( )
如图,菱形ABCD的边长为15cm,对角线AC=24cm,DH⊥AB于H,则DH的长为( )| A、14.4cm |
| B、16.2cm |
| C、15.4cm |
| D、18.2cm |
为了解某校初三年级500名学生800米跑的成绩,从中抽取了100名学生的800米跑成绩进行统计.下列说法错误的是( )
| A、这种调查方式是抽样调查 |
| B、每名学生的800米跑成绩是个体 |
| C、100名学生是总体的一个样本 |
| D、100是样本容量 |
在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且满足∠A:∠B:∠C=1:2:3,则△ABC一定是( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不能确定 |