Question

15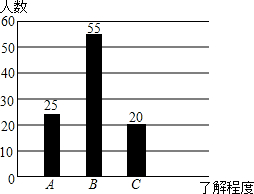．某中学组织学生开展社会实践活动，调查某社区居民对消防知识的了解程度（A：特别熟悉，B：有所了解，C：不知道），在该社区随机抽取了100名居民进行问卷调查，将调查结果制成如图所示的统计图，根据统计图解答下列问题：
（1）若该社区有居民900人，试估计对消防知识“特别熟悉”的居民人数；
（2）该社区的管理人员有男、女各2名，若从中选2名参加消防知识培训，试用列表或画树状图的方法，求恰好选中一男一女的概率．

Answer 1

分析 （1）根据条形统计图可以估算出该社区对消防知识“特别熟悉”的居民的人数；
（2）根据题意可以写出相应的列表或树状图，从而可以求得恰好选中一男一女的概率．

解答 解：（1）在调查的居民中，对消防知识“特别熟悉”的居民所占的百分比为：$\frac{25}{100}$×100%=25%，
该社区对消防知识“特别熟悉”的居民估计有：900×25%=225（人），
即该社区对消防知识“特别熟悉”的居民人数估计为225；
（2）记A₁、A₂表示两个男性管理人员，B₁，B₂表示两个女性管理人员，列表或树状图如下：

故恰好选中一男一女的概率为：$\frac{8}{12}$=$\frac{2}{3}$，
即恰好选中一男一女的概率是$\frac{2}{3}$．

点评 本题考查列表法与树状图法、条形统计图、用样本估计总体，解题的关键是明确题意，找出所求问题需要的条件，可以列出表格或写出树状图，求出所求问题的概率．