题目内容
20．若a＞b，则下列不等式一定成立的是（ ）| A． | a+b＞b | B． | $\frac{b}{a}$＞1 | C． | ac2＞bc2 | D． | b-a＜0 |
分析 根据不等式的性质①不等式的两边同时加上（或减去）同一个数或同一个含有字母的式子，不等号的方向不变；②不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变；③不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变进行分析即可．
解答 解：A、当b＜a＜0，则a+b＜b，故此选项错误；
B、当a＞0，b＜0，$\frac{b}{a}$＜，1故此选项错误；
C、当c=0，ac2＞bc2，故此选项错误；
D、当a＞b，b-a＜0，故此选项正确；
故本题选D．
点评 此题主要考查了不等式的性质，关键是掌握不等式的性质．
练习册系列答案
相关题目
如图所示，沿DE折叠矩形ABCD的一边，使点C落在AB边上的点F处，若AD=8，且△AFD的面积为60，求CE的长．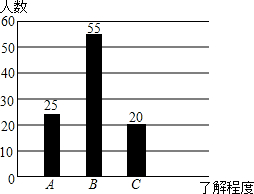
某中学组织学生开展社会实践活动，调查某社区居民对消防知识的了解程度（A：特别熟悉，B：有所了解，C：不知道），在该社区随机抽取了100名居民进行问卷调查，将调查结果制成如图所示的统计图，根据统计图解答下列问题：
5．下列各式，计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | 3$\sqrt{2}-\sqrt{2}$=3 | C． | 2$\sqrt{3}×3\sqrt{3}=6\sqrt{3}$ | D． | （$\sqrt{8}-\sqrt{6}$）$÷\sqrt{2}=2-\sqrt{3}$ |
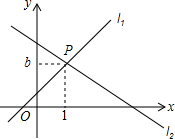如图，直线l1：y=x+1与直线l2：y=mx+n相交于点P（1，b）．