题目内容
18.已知反比例函数y=$\frac{n+3}{x}$的图象,在第一象限内y随x的增大而减小,则n的取值范围是n>-3.分析 由于反比例函数y=$\frac{n+3}{x}$的图象在每个象限内y的值随x的值增大而减小,可知比例系数为正数,据此列出不等式解答即可.
解答 解:∵反比例函数y=$\frac{n+3}{x}$的图象在每个象限内y的值随x的值增大而减小,
∴n+3>0,
解得n>-3.
故答案为n>-3.
点评 本题考查了反比例函数的性质,要知道:(1)k>0,反比例函数图象在一、三象限,在每个象限内y的值随x的值增大而减小;(2)k<0,反比例函数图象在第二、四象限内,在每个象限内y的值随x的值增大而增大.

练习册系列答案
相关题目
10.计算:6x+7x的结果是( )
| A. | 13x | B. | 7x | C. | 6x | D. | x |
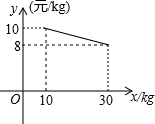 某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.
某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.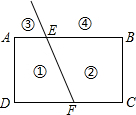 如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).
如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).