题目内容
8.在△ABC中,∠CAB+2∠ABC=90°,点D为AB边中点,连接CD,若∠DCB=45°,AB=2$\sqrt{10}$,则CD=2.分析 作∠CAB平分线根据∠CAB+2∠ABC=90°、∠DCB=45°可得AE⊥CD;由点D为AB边中点知AC=AD;过点D作DF∥AE交BC于点F结合D为AB中点、M是CD中点可得CE=EF=BF,设CM=x分别表示出DE、EN、DN的长,根据DC=DF、CE=EF知∠DEN=90°,在RT△DEN中,根据勾股定理求得x的值即可.
解答 解:作∠CAB平分线AE交CD于M,交BC于E,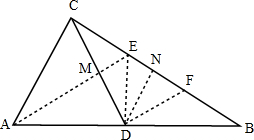
∵∠CAB+2∠ABC=90°,
∴$\frac{1}{2}$∠CAB+∠ABC=∠CEA=45°,
∵∠DCB=45°,
∴AE⊥CD,
∵点D为AB边中点,AB=2$\sqrt{10}$
∴AC=AD=$\sqrt{10}$,
过点D作DF∥AE交BC于点F,
∵AD=BD,CM=DM,
∴EF=BF,CE=EF,
∴CE=EF=BF,
设CM=x,则CE=$\sqrt{2}$x,CD=DF=2x,
取BC中点N,连接DE、DN,
则DN=$\frac{1}{2}$AC=$\frac{\sqrt{10}}{2}$,DE=$\sqrt{2}$x,EN=$\frac{\sqrt{2}}{2}$x,
∵DC=DF,CE=EF,
∴∠DEN=90°,
故DE2+EN2=DN2,即($\sqrt{2}$x)2+($\frac{\sqrt{2}}{2}$x)2=($\frac{\sqrt{10}}{2}$)2,
解得:x=1,
则CD=2x=2.
故答案为:2.
点评 本题主要考查了等腰三角形性质、中位线定理及勾股定理的运用,根据题意构造出直角三角形是解题的出发点,表示出所需线段的长度并运用到直角三角形中是关键.

练习册系列答案
相关题目
16.一次函数y=x-1的图象向上平移2个单位后,不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.计算:(-1)100×5的结果是( )
| A. | -1 | B. | 5 | C. | 100 | D. | 500 |
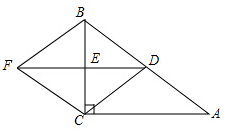 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC.