题目内容
12.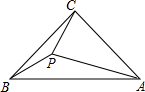 如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.
如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.
分析 以PC为边在△ACP内作等边三角形△PCQ,连接AQ,由△BCP≌△ACQ推出∠QCA=∠QAC=15°、QA=QC=QP,再证明∠PQA=150°得∠QPA=∠QAP=15°,可以得∠APC=∠ACP=75°,所以PA=AC,由此解决问题.
解答 解:如图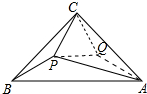 以PC为边在△ACP内作等边三角形△PCQ,连接AQ.
以PC为边在△ACP内作等边三角形△PCQ,连接AQ.
∵∠ACB=90°,∠PCQ=60°,∠BCP=∠PBC=15°,
∴∠ACQ=∠ACQ=15°,PC=PB,CP=CQ,
在△BCP和△ACQ中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCP=∠ACQ}\\{CP=CQ}\end{array}\right.$,
∴△BCP≌△ACQ,
∴∠CBP=∠CAQ=15°=∠ACQ,
∴QC=QA=PQ,∠CQA=180°-∠QCA-∠QAC=150°,
∵∠PQA=360°-∠PQC-∠AQC=150°,
∴∠QPA=∠QAP=15°,
∴∠APC=∠CPQ+∠APQ=75°,∠PCA=90°-∠BCP=75°,
∴∠APC=∠ACP,
∴PA=AC=4.
故答案为4.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、等边三角形的性质等知识,作等边三角形△PCQ,构造全等三角形是解决问题的关键,题目有点难度.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
2.从2010年以来,我省中考报名人数逐年递减,2015年全省只有56.65万考生参加中考,其中56.65万用科学记数法表示为( )
| A. | 56.65×104 | B. | 5.665×105 | C. | 5.656×106 | D. | 0.5665×107 |
4.等腰三角形的两边分别为7cm和4cm,则它的周长是( )
| A. | 15cm | B. | 15cm或18cm | C. | 18cm | D. | 11cm |
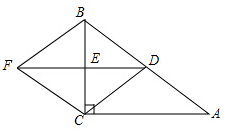 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC. 如图,在四边形ABCD中,AB=CD=6,BC=AD=8,AC=10.求证:四边形ABCD是矩形.
如图,在四边形ABCD中,AB=CD=6,BC=AD=8,AC=10.求证:四边形ABCD是矩形.