题目内容
15.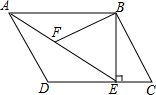 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;
(2)若AB=4,BE=3,AD=$\frac{7}{2}$,求BF的长.
分析 (1)求三角形相似就要得出两组对应的角相等,已知了∠BFE=∠C,根据等角的补角相等可得出∠ADE=∠AFB,根据AB∥CD可得出∠BAF=∠AED,这样就构成了两三角形相似的条件.
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,这样就能求出BF的长了.
解答 (1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
∵△ABF∽△EAD,
∴$\frac{BF}{AD}$=$\frac{AB}{AE}$,
∴$\frac{BF}{\frac{7}{2}}$=$\frac{4}{5}$.
∴BF=$\frac{14}{5}$.
点评 本题主要考查了相似三角形的判定和性质,平行四边形的性质,等角的补角,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
10.已知一元二次方程ax2-2x+1=0没有实数根,则抛物线y=ax2-2x+1的顶点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
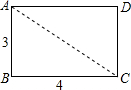 如图,一矩形纸片ABCD,用剪刀沿虚线AC将该纸片剪成两块三角形,现要用剪得的两块三角形拼接成一个等腰三角形,请设计两种不同的方法,并将两种拼法画在方框中,要求在图中标明用于拼接的直角三角形的三边长.
如图,一矩形纸片ABCD,用剪刀沿虚线AC将该纸片剪成两块三角形,现要用剪得的两块三角形拼接成一个等腰三角形,请设计两种不同的方法,并将两种拼法画在方框中,要求在图中标明用于拼接的直角三角形的三边长.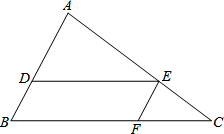 如图,在△ABC中,DE∥BC,EF∥AB.
如图,在△ABC中,DE∥BC,EF∥AB.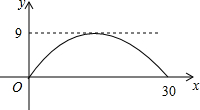 有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.
有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.