题目内容
9.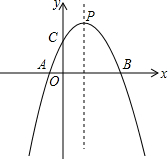 如图,抛物线y=-x2+bx+c的对称轴是直线x=1,与y轴交于点C(0,3),与x轴交于 A,B两点.
如图,抛物线y=-x2+bx+c的对称轴是直线x=1,与y轴交于点C(0,3),与x轴交于 A,B两点.(1)请写出这个抛物线的解析式;
(2)若此抛物线与x轴交于A,B两点,顶点是P,求△ABP的面积.
参考公式:顶点坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)
分析 (1)根据对称轴公式,以及图象经过点(0,3),即可列方程组求得b、c的值,得到函数解析式;
(2)在抛物线解析式中令y=0求得A和B的横坐标,求得AB的长,然后利用配方法求得P的坐标,则根据三角形面积公式求解.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{-\frac{b}{-2}=1}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
则抛物线的解析式是y=-x2+2x+3;
(2)在y=-x2+2x+3中令y=0,得-x2+2x+3=0,
解得:x1=-1,x2=3.
则A的坐标是(-1,0),B的坐标是(3,0),则AB=4,
y=-x2+2x+3=-(x-1)2+4,
则顶点P的坐标是(1,4).
则S△ABP=$\frac{1}{2}$×4×4=8.
点评 本题考查了待定系数法求函数的解析式以及抛物线与坐标轴的交点的求法,求得函数解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
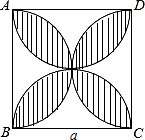 如图,正方形的边长为a,以各边为直径在正方形内画半圆.
如图,正方形的边长为a,以各边为直径在正方形内画半圆. 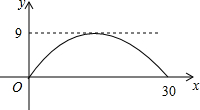 有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.
有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.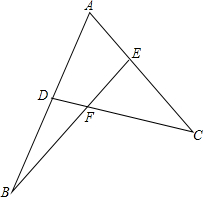 如图:∠ADC+∠AEB=180°,AB=k•AC,判断BE与CD的关系,并加以证明.
如图:∠ADC+∠AEB=180°,AB=k•AC,判断BE与CD的关系,并加以证明.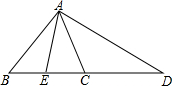 如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.
如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.